题目内容
若
，则
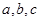的大小关系为
A． | B． | C． | D． |
A
解析试题分析：
，
, 
，所以
,故选A.
考点：对数函数的性质
点评：比较大小一般的思路是先研究函数的单调性，再结合不等式的性质来求解，属于基础题。
练习册系列答案
相关题目
对于使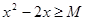
成立的所有常数M中，我们把M的最大值－1，称为函数
的“下确界”，若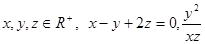
的“下确界”为
| A．8 | B．6 | C． 4 | D．1 |
已知正数
的最小值为
A． | B． | C． | D． |
设A=
， B=
, 则A与B的大小关系是
| A．A<B | B．A>B | C．仅有x>0,A<B | D．以上结论都不成立 |
设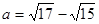
，
，
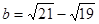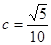，则
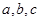的大小关系为
A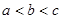． | B． | C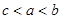． | D． |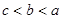
已知
，那么下列判断中正确的是（ ）
A． | B． | C． | D． |
若a>b>c，则下列不等式成立的是（ ）
A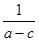． > | B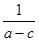．< | C．ac>bc | D．ac<bc |
已知
，且
，则下列不等式中，正确的是 （ ）
A． | B． |
C． | D． |
设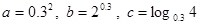
，则
A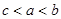． | B． |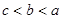
C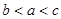． | D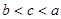． |