题目内容
已知f（x）是奇函数，在（－1，1）上是减函数，且满足f（1－a）＋f（1－a2）＜0，求实数a的范围.?
解：要求a的取值范围，先要列出关于a的不等式，这需要根据原条件，然后根据减函数的定义由函数值逆推出自变量的关系.
由f（1－a）＋f（1－a2）＜0，得f（1－a）＜－f（1－a2）.?
∵f（x）是奇函数，∴－f（1－a2）=f（a2－1）.?
于是f（1－a）＜f（a2－1）.?
又由于f（x）在（－1，1）上是减函数，因此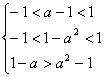
解之，得0＜a＜1.
练习册系列答案
相关题目