题目内容
 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD的中点.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD的中点.(1)求证:SB∥平面EAC;
(2)求点D到平面EAC的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)画出图形,证明平面EAC外的直线SB与平面内的直线EO平行,即可证明SB∥平面EAC;
(2)作出点D到平面EAC的距离,通过解三角形求解距离即可.
(2)作出点D到平面EAC的距离,通过解三角形求解距离即可.
解答:
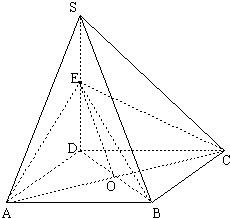 解:(1)证明:连接BD交AC于点O,连接EO.
解:(1)证明:连接BD交AC于点O,连接EO.
∵底面ABCD是正方形,
∴O是BD的中点.
又∵E是SD的中点,
∴EO∥SB.
又∵EO?平面EAC,SB?平面EAC,
∴SB∥平面EAC.
(2)∵ABCD是正方形,∴DB⊥AC
SD⊥平面ABCD,∴AC⊥平面DOE,
∴平面DOE⊥平面ACE,
作DF⊥OE于F,则OF就是点D到平面EAC的距离.
∵SD=AD=a,点E是SD的中点,
∴DE=
a,DO=
a,
∴OE=
=
=
a.
DF=
=
=
a.
∴点D到平面EAC的距离
a.
 解:(1)证明:连接BD交AC于点O,连接EO.
解:(1)证明:连接BD交AC于点O,连接EO.∵底面ABCD是正方形,
∴O是BD的中点.
又∵E是SD的中点,
∴EO∥SB.
又∵EO?平面EAC,SB?平面EAC,
∴SB∥平面EAC.
(2)∵ABCD是正方形,∴DB⊥AC
SD⊥平面ABCD,∴AC⊥平面DOE,
∴平面DOE⊥平面ACE,
作DF⊥OE于F,则OF就是点D到平面EAC的距离.
∵SD=AD=a,点E是SD的中点,
∴DE=
| 1 |
| 2 |
| ||
| 2 |
∴OE=
| DE2+DO2 |
(
|
| ||
| 2 |
DF=
| DE•D0 |
| OE |
| ||||||
|
| ||
| 6 |
∴点D到平面EAC的距离
| ||
| 6 |
点评:本题考查直线与平面平行,直线与直线的垂直,考查学生转化思想,逻辑思维能力,是中档题.

练习册系列答案
相关题目
若连续抛两次骰子分别所得的点数a,b作为点P的横、纵坐标,则点P在直线x+y=5下方的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
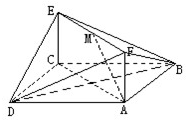 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=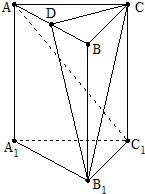 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.