Question

下图为某四棱锥的展开图,其中ABCD是边长为a的正方形,SA=PA=a,DR=SD,

BQ=BP且点S、A、B、Q及P、A、D、R共线,沿虚线将它们折叠成四棱锥,使P、Q、R、S四点重合为S.

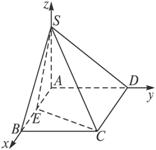
(1)请画出四棱锥S—ABCD的示意图,并证明SA⊥底面ABCD;

(2)若E为AB中点,求二面角ESCD的大小;

(3)求D到面SEC的距离.

Answer 1

解：(1)如图,SA⊥AD,SA⊥AB,SA⊥平面ABCD.

    (2)建立如图所示的坐标系,则E(,0,0),D(0,a,0),C(a,a,0),S(0,0,a)

    设面SEC的法向量为n=(x,y,z).

   

    令z=1,得n=(2,-1,1),同理可求得平面SCD的法向量m=(0,1,1).

    cos〈m,n〉==0,故〈m,n〉=90°,

    即E-SC-D的大小为90°.

    (3)D到面SEC的距离d===a,

    也可用·a²·a=V_S—CDE=V_D—SEC=·()²··d,

    求得d=a.