题目内容
(理)已知点 是圆
是圆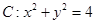 上的动点.
上的动点.
(1)求点 到直线
到直线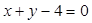 的距离的最小值;
的距离的最小值;
(2)若直线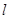 与圆
与圆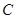 相切,且
相切,且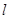 与x,y轴的正半轴分别相交于
与x,y轴的正半轴分别相交于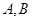 两点,求
两点,求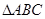 的面积最小时直线
的面积最小时直线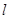 的方程;
的方程;
【答案】
(1) (2)
(2)
【解析】
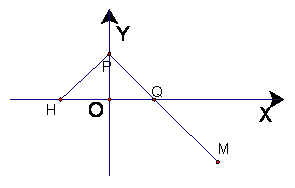
试题分析:解:(1)圆心到直线l的距离为 , 所以P到直线l:
, 所以P到直线l: 的距离的最小值为:
的距离的最小值为:
(2)设直线l的方程为: ,因为l与x,y轴的正半轴分别相交于A,B两点,则
,因为l与x,y轴的正半轴分别相交于A,B两点,则 ,
,
且 ,又l与圆C相切,则C点到直线l的距离等于圆的半径2,
,又l与圆C相切,则C点到直线l的距离等于圆的半径2,
即: , ①,
, ①,
而 ②
②
将①代入②得 ,
,
当且仅当 时取等号,所以当
时取等号,所以当 时,
时,  的面积最小,此时
的面积最小,此时 ,直线l的方程为:
,直线l的方程为:
考点:本试题考查了点到直线的距离和三角形面积问题。
点评:解决该试题中圆上点到直线的距离的最值问题,直接转化为圆心到直线的距离加上圆的半径为最大值,减去圆的半径为最小值得到。这是高考中常考的一个知识点,要熟练的掌握。

练习册系列答案
相关题目

 是圆
是圆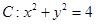 上的动点.
上的动点. 的距离的最小值;
的距离的最小值; 与圆
与圆 相切,且
相切,且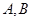 两点,求
两点,求 的面积最小时直线
的面积最小时直线