题目内容
以下四个命题中,真命题的个数有( )
(1)?x∈R,x2+3≥0;
(2)?x∈N,x2>0;
(3)?x∈Z,使x5<1;
(4)?x∈Q,x2=3.
(1)?x∈R,x2+3≥0;
(2)?x∈N,x2>0;
(3)?x∈Z,使x5<1;
(4)?x∈Q,x2=3.
分析:根据平方非负的性质,得到(1)正确;而(2)可以举出反例,说明它不正确;通过举例说明,得到(3)正确;根据无理数的定义,得到(4)不正确.
解答:解:因为x2≥0,所以?x∈R,x2+3≥3≥0,故(1)正确;
因为存在自然数x=0,x2>0不成立,故(2)不正确;
因为存在整数x=-1,使x5<1成立,故(3)正确;
因为(±
)2=3,满足x2=3的x只有±
,是无理数
∴不存在有理数,使x2=3,故(4)不正确.
这样,正确的是(1)(3),两个
故选B
因为存在自然数x=0,x2>0不成立,故(2)不正确;
因为存在整数x=-1,使x5<1成立,故(3)正确;
因为(±
| 3 |
| 3 |
∴不存在有理数,使x2=3,故(4)不正确.
这样,正确的是(1)(3),两个
故选B
点评:本题给出全称命题和特称命题,叫我们判断命题的真假.着重考查了实数、整数和自然数的性质和含有量词的命题等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知-
<θ<
,且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,在以下四个答案中,可能正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
 ,且
,且 其中
其中 ,则关于
,则关于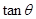 的值,在以下四个答案中,可能正确的是 (
)
的值,在以下四个答案中,可能正确的是 (
) B.3 或
B.3 或 C.
C. D.
D.


