题目内容
在△ABC中，tanAtanB＞1，则△ABC是________．
锐角三角形
分析：利用两角和的正切函数公式表示出tan（A+B），根据A与B的范围以及tanAtanB＞1，得到tanA和tanB都大于0，即可得到A与B都为锐角，然后判断出tan（A+B）小于0，得到A+B为钝角即C为锐角，所以得到此三角形为锐角三角形．
解答：因为A和B都为三角形中的内角，
由tanAtanB＞1，得到1-tanAtanB＜0，
且得到tanA＞0，tanB＞0，即A，B为锐角，
所以tan（A+B）=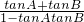
＜0，
则A+B∈（
，π），即C都为锐角，
所以△ABC是锐角三角形．
故答案为：锐角三角形
点评：此题考查学生灵活运用两角和的正切函数公式化简求值，是一道基础题．本题的关键是得到tanA和tanB都大于0，进而得到A和B都为锐角．
分析：利用两角和的正切函数公式表示出tan（A+B），根据A与B的范围以及tanAtanB＞1，得到tanA和tanB都大于0，即可得到A与B都为锐角，然后判断出tan（A+B）小于0，得到A+B为钝角即C为锐角，所以得到此三角形为锐角三角形．
解答：因为A和B都为三角形中的内角，
由tanAtanB＞1，得到1-tanAtanB＜0，
且得到tanA＞0，tanB＞0，即A，B为锐角，
所以tan（A+B）=
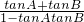＜0，则A+B∈（
，π），即C都为锐角，所以△ABC是锐角三角形．
故答案为：锐角三角形
点评：此题考查学生灵活运用两角和的正切函数公式化简求值，是一道基础题．本题的关键是得到tanA和tanB都大于0，进而得到A和B都为锐角．
练习册系列答案
相关题目
，
＝0，则过点C，以A、H为两焦点的椭圆的离心率为
＝
，
＝0，
＝0，则过点C，以A、H为两焦点的椭圆的离心率为
=2sinC。