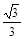题目内容
一个球与一个正三棱柱的三个侧面和两个底面均相切，已知球的体积是
π，那么这个三棱柱的体积是（ ）
A．96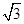 | B．16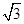 | C．24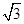 | D．48 |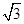
D
解析
练习册系列答案
手拉手全优练考卷系列答案
相关题目
一个几何体的三视图如右图所示则,该几何体的体积为 【 】
A． | B． |
C． | D． |
在正三棱锥中，相邻两侧面所成二面角的取值范围是
A． | B． |
C．（0， ） | D． |
某几何体的正视图和侧视图均为如图1所示，则在图2的四个图中可以作为该几何体的俯视图的是（ ）
| A．（1），（3） | B．（1），（4） |
| C．（2），（4） | D．（1），（2），（3），（4） |
设三棱柱的侧棱垂直于底面，所有棱长都为
，顶点都在一个球面上，则该球的表面积为（ ）
A． | B． | C． | D． |
若平行于圆锥底面的平面将圆锥的高平分，则圆锥被分成的两部分的侧面积比是 （ ）
| A．1:1 | B．1:2 | C．1:3 | D．1:4 |