题目内容
已知函数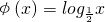 与函数g(x)的图象关于y=x对称,若g(a)g(b)=2,且a<0,b<0,则
与函数g(x)的图象关于y=x对称,若g(a)g(b)=2,且a<0,b<0,则 +
+ 的最大值为________.
的最大值为________.
-9
分析:依题意可求得g(x)= ,于是有a+b=-1,利用基本不等式即可求得答案.
,于是有a+b=-1,利用基本不等式即可求得答案.
解答:∵φ(x)= 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,
∴φ(x)= 与函数g(x)互为反函数,
与函数g(x)互为反函数,
∴g(x)= ,
,
∵g(a)g(b)=2,
∴ •
• =
= =2,
=2,
∴a+b=-1,又a<0,b<0,
∴ +
+ =-(
=-( +
+ )(a+b)=-(4+
)(a+b)=-(4+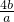 +
+ +1)
+1)
依题意,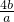 +
+ ≥2
≥2 =4,
=4,
∴-(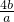 +
+ )≤-4,
)≤-4,
∴-(4+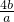 +
+ +1)≤-9.
+1)≤-9.
故答案为:-9.
点评:本题考查反函数与基本不等式的应用,求得a+b=-1是关键,属于中档题.
分析:依题意可求得g(x)=
 ,于是有a+b=-1,利用基本不等式即可求得答案.
,于是有a+b=-1,利用基本不等式即可求得答案.解答:∵φ(x)=
 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,∴φ(x)=
 与函数g(x)互为反函数,
与函数g(x)互为反函数,∴g(x)=
 ,
,∵g(a)g(b)=2,
∴
 •
• =
= =2,
=2,∴a+b=-1,又a<0,b<0,
∴
 +
+ =-(
=-( +
+ )(a+b)=-(4+
)(a+b)=-(4+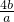 +
+ +1)
+1)依题意,
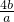 +
+ ≥2
≥2 =4,
=4,∴-(
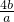 +
+ )≤-4,
)≤-4,∴-(4+
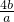 +
+ +1)≤-9.
+1)≤-9.故答案为:-9.
点评:本题考查反函数与基本不等式的应用,求得a+b=-1是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称, 的最大值为
的最大值为  =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 . 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).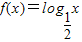 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,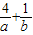 的最大值为
的最大值为 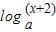 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 . 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).