题目内容
设函数f(x)=x2-2(-1)klnx(k∈N*).f′(x)是f(x)的导函数.
(1)当k为偶数时,正项数列{an}满足: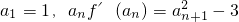 .证明:数列
.证明:数列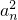 中任意不同三项不能构成等差数列;
中任意不同三项不能构成等差数列;
(2)当k为奇数时,证明:当x>0时,对任意正整数n都有[f′(x)]n-2n-1f′(x)≥2n(2n-2)成立.
证明:(1)当k为偶数时,f(x)=x2-2lnx,f′(x)=2x- =
= ,f′(an)=
,f′(an)=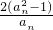
由已知,得出2( -1)=
-1)= -3,
-3,
∴ +1=2(
+1=2( +1),数列{
+1),数列{ +1}是以2为公比,以
+1}是以2为公比,以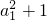 =2为首项的等比数列.
=2为首项的等比数列.
∴ +1=2•2n-1=2n,
+1=2•2n-1=2n, =2n-1,
=2n-1,
假设数列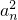 中存在不同三项
中存在不同三项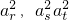 构成等差数列,不妨设r<s<t,则
构成等差数列,不妨设r<s<t,则 ,即2(2s-1)=2r-1+2t-1,2s+1=2r+2t,2s-r+1=1+2t-r
,即2(2s-1)=2r-1+2t-1,2s+1=2r+2t,2s-r+1=1+2t-r
又s-r+1>0,t-r>0,
∴2s-r+1为偶数,1+2t-r为奇数,矛盾.故假设不成立.因此数列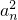 中任意不同三项不能构成等差数列.
中任意不同三项不能构成等差数列.
(2)当k为奇数时,f(x)=x2+2lnx,f′(x)=2x+ =2(
=2( ),即证
),即证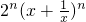 -2n-1•2(
-2n-1•2(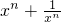 )≥2n(2n-2)
)≥2n(2n-2)
即证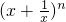 -(
-(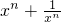 )≥2n-2.
)≥2n-2.
证法一:由二项式定理,即证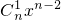 +
+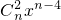 +
+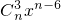 +…
+…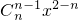 ≥2n-2
≥2n-2
设Sn=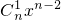 +
+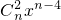 +
+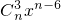 +…
+…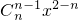 ,
,
又Sn=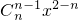 +
+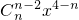 +…+
+…+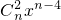 +
+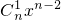 .
.
两式相加,得出2Sn= +
+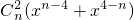 +…+
+…+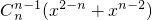
≥2(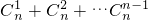 )=2(2n-2).
)=2(2n-2).
∴Sn≥2n-2.
证法二:数学归纳法
当n=1时,左边=0,右边=0,不等式成立.
设当n=k(k≥1)时成立.即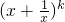 -(
-(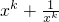 )≥2k-2成立,
)≥2k-2成立,
则当n=k+1时, -(
-(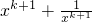 )=
)=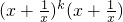 -(
-(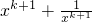 )
)
≥[(2k-2)+(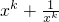 )]
)] -(
-(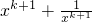 )
)
=(2k-2) +
+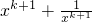 +xk-1+
+xk-1+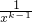 -(
-(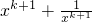 )
)
=(2k-2) +xk-1+
+xk-1+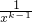
≥(2k-2)•2+2
=2k+1-2
即当n=k+1时不等式成立.
综上所述,对任意正整数n不等式成立.
分析:(1)当k为偶数时,由已知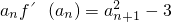 ,得出2(
,得出2( -1)=
-1)= -3,整理构造得出数列{
-3,整理构造得出数列{ +1}是以2为公比,以
+1}是以2为公比,以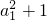 =2为首项的等比数列,求出
=2为首项的等比数列,求出 =2n-1,假设数列
=2n-1,假设数列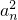 中存在不同三项
中存在不同三项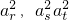 构成等差数列,不妨设r<s<t,则
构成等差数列,不妨设r<s<t,则 ①,考察①是否有解,作出解答.
①,考察①是否有解,作出解答.
(2)当k为奇数时,原不等式化为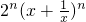 -2n-1•2(
-2n-1•2(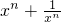 )≥2n(2n-2).可以利用二项式定理,结合倒序相加法,基本不等式进行证明,或者用数学归纳法证明.
)≥2n(2n-2).可以利用二项式定理,结合倒序相加法,基本不等式进行证明,或者用数学归纳法证明.
点评:本题是函数、数列、不等式的综合.考查数列通项公式求解,不定方程解的讨论,不等式的证明方法.用到了构造转化、基本不等式、数学归纳法等知识方法.运算量较大,是容易出错的地方.
 =
= ,f′(an)=
,f′(an)=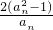
由已知,得出2(
 -1)=
-1)= -3,
-3,∴
 +1=2(
+1=2( +1),数列{
+1),数列{ +1}是以2为公比,以
+1}是以2为公比,以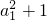 =2为首项的等比数列.
=2为首项的等比数列.∴
 +1=2•2n-1=2n,
+1=2•2n-1=2n, =2n-1,
=2n-1,假设数列
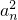 中存在不同三项
中存在不同三项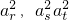 构成等差数列,不妨设r<s<t,则
构成等差数列,不妨设r<s<t,则 ,即2(2s-1)=2r-1+2t-1,2s+1=2r+2t,2s-r+1=1+2t-r
,即2(2s-1)=2r-1+2t-1,2s+1=2r+2t,2s-r+1=1+2t-r又s-r+1>0,t-r>0,
∴2s-r+1为偶数,1+2t-r为奇数,矛盾.故假设不成立.因此数列
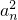 中任意不同三项不能构成等差数列.
中任意不同三项不能构成等差数列.(2)当k为奇数时,f(x)=x2+2lnx,f′(x)=2x+
 =2(
=2( ),即证
),即证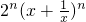 -2n-1•2(
-2n-1•2(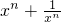 )≥2n(2n-2)
)≥2n(2n-2)即证
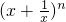 -(
-(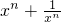 )≥2n-2.
)≥2n-2.证法一:由二项式定理,即证
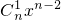 +
+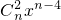 +
+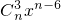 +…
+…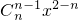 ≥2n-2
≥2n-2设Sn=
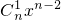 +
+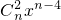 +
+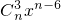 +…
+…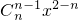 ,
,又Sn=
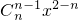 +
+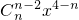 +…+
+…+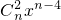 +
+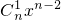 .
.两式相加,得出2Sn=
 +
+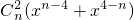 +…+
+…+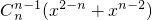
≥2(
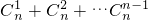 )=2(2n-2).
)=2(2n-2).∴Sn≥2n-2.
证法二:数学归纳法
当n=1时,左边=0,右边=0,不等式成立.
设当n=k(k≥1)时成立.即
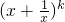 -(
-(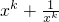 )≥2k-2成立,
)≥2k-2成立,则当n=k+1时,
 -(
-(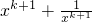 )=
)=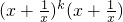 -(
-(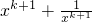 )
)≥[(2k-2)+(
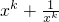 )]
)] -(
-(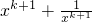 )
)=(2k-2)
 +
+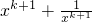 +xk-1+
+xk-1+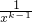 -(
-(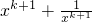 )
)=(2k-2)
 +xk-1+
+xk-1+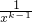
≥(2k-2)•2+2
=2k+1-2
即当n=k+1时不等式成立.
综上所述,对任意正整数n不等式成立.
分析:(1)当k为偶数时,由已知
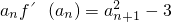 ,得出2(
,得出2( -1)=
-1)= -3,整理构造得出数列{
-3,整理构造得出数列{ +1}是以2为公比,以
+1}是以2为公比,以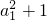 =2为首项的等比数列,求出
=2为首项的等比数列,求出 =2n-1,假设数列
=2n-1,假设数列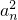 中存在不同三项
中存在不同三项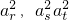 构成等差数列,不妨设r<s<t,则
构成等差数列,不妨设r<s<t,则 ①,考察①是否有解,作出解答.
①,考察①是否有解,作出解答.(2)当k为奇数时,原不等式化为
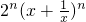 -2n-1•2(
-2n-1•2(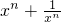 )≥2n(2n-2).可以利用二项式定理,结合倒序相加法,基本不等式进行证明,或者用数学归纳法证明.
)≥2n(2n-2).可以利用二项式定理,结合倒序相加法,基本不等式进行证明,或者用数学归纳法证明.点评:本题是函数、数列、不等式的综合.考查数列通项公式求解,不定方程解的讨论,不等式的证明方法.用到了构造转化、基本不等式、数学归纳法等知识方法.运算量较大,是容易出错的地方.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目