题目内容
已知抛物线C：y=2x2，直线：y=kx+2交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交C于点N．
证明：抛物线C在点N处的切线与AB平行．
证明：抛物线C在点N处的切线与AB平行．
分析：把y=kx+2代入y=2x2，利用韦达定理，确定N的坐标，从而可得抛物线在点N处的切线l的方程，进而可证明切线l的与k相等，即可得到结论．
解答：证明：如图，设A（x1，2
），B（x2，2
），
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
，x1x2=-1，所以xN=xM=
=
，
即N点的坐标为（
，
）．
设抛物线在点N处的切线l的方程为y-
=m（x-
），
将y=2x2代入上式得：2x2-mx+
-
=0，
因为直线l与抛物线C相切，所以△=m2-8（
-
）=m2-2mk+k2=（m-k）2=0，
所以m=k，即l∥AB．
| x | 2 1 |
| x | 2 2 |
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
| k |
| 2 |
| x1+x2 |
| 2 |
| k |
| 4 |
即N点的坐标为（
| k |
| 4 |
| k2 |
| 8 |
设抛物线在点N处的切线l的方程为y-
| k2 |
| 8 |
| k |
| 4 |
将y=2x2代入上式得：2x2-mx+
| mk |
| 4 |
| k2 |
| 8 |
因为直线l与抛物线C相切，所以△=m2-8（
| mk |
| 4 |
| k2 |
| 8 |
所以m=k，即l∥AB．
点评：本题考查直线与抛物线的位置关系，考查韦达定理的运用，考查抛物线的切线，属于中档题．
练习册系列答案
相关题目
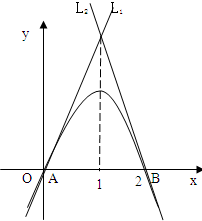已知抛物线C：y=-x2+2x，在点A（0，0），B（2，0）分别作抛物线的切线L1、L2．
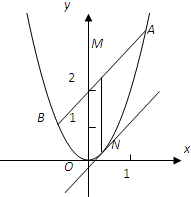已知抛物线C：y=2x2，直线y=kx+2交C于A，B两点，M是线段AB的中点，过M作轴的垂线交C于点N．