题目内容
下列命题中,真命题的是( )
分析:对于A,sinx+cosx=
sin(x+
),根据x∈[0,
],可得sinx+cosx=
sin(x+
)∈[1,
];
对于B,x=0不成立;
对于C,根据x>3,可得x2-3x+1=(x-
)2-
=9-9+1=1>0;
对于D,?x∈(
,π),tanx<0,sinx>0,故可得结论.
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
对于B,x=0不成立;
对于C,根据x>3,可得x2-3x+1=(x-
| 3 |
| 2 |
| 5 |
| 4 |
对于D,?x∈(
| π |
| 2 |
解答:解:对于A,sinx+cosx=
sin(x+
),∵x∈[0,
],∴x+
∈[
,
]
∴sin(x+
)∈[
,1],∴sinx+cosx=
sin(x+
)∈[1,
],故A为假命题;
对于B,x=0不成立;
对于C,x2-3x+1=(x-
)2-
,∵x>3,∴x2-3x+1=(x-
)2-
=9-9+1=1>0,故C为真命题;
对于D,?x∈(
,π),tanx<0,sinx>0,故为假命题
综上,真命题为C
故选C.
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴sin(x+
| π |
| 4 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| 2 |
对于B,x=0不成立;
对于C,x2-3x+1=(x-
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
对于D,?x∈(
| π |
| 2 |
综上,真命题为C
故选C.
点评:本题考查命题真假的判断,解题的关键是确定三角函数的值域,正确判断三角函数的符号,属于中档题.

练习册系列答案
相关题目
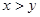 ,则
,则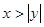 ”的逆命题
”的逆命题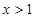 ,则
,则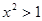 ”的否命题
”的否命题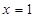 ,则
,则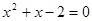 ”的否命题
”的否命题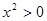 ,则
,则