题目内容
已知数列{an}为递增的等比数列，其中a2=9，a1+a3=30．（1）求数列{an}的通项公式；
（2）若bn=2an+1，求数列{bn}的前n项和Sn．
【答案】分析：（1）由 a2=9，a1+a3=30，利用等比数列的通项公式表示已知，解方程可求q，进而可求
（2）由（1）可得bn=2an+1=2•3n+1，利用分组求和，结合等比数列的求和公式即可求解
解答：解：（1）设等比数列的公比为q
又由已知 a2=9，a1+a3=30
可得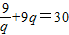
，解得
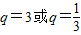
由已知，数列为递增数列，所以可知q=3
即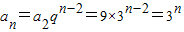
（2）∵bn=2an+1=2•3n+1
∴
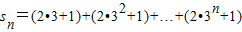
=2（3+32+…+3n）+n
=
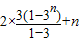
=3n+1+n-3
∴数列{bn}的前n项和Sn为3n+1+n-3
点评：本题主要考查了等比数列的通项公式及求和公式的 应用，数列求和方法中的分组求和方法的应用
（2）由（1）可得bn=2an+1=2•3n+1，利用分组求和，结合等比数列的求和公式即可求解
解答：解：（1）设等比数列的公比为q
又由已知 a2=9，a1+a3=30
可得
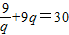，解得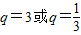由已知，数列为递增数列，所以可知q=3
即
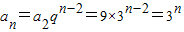
（2）∵bn=2an+1=2•3n+1
∴
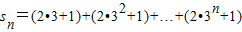
=2（3+32+…+3n）+n
=
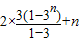
=3n+1+n-3
∴数列{bn}的前n项和Sn为3n+1+n-3
点评：本题主要考查了等比数列的通项公式及求和公式的 应用，数列求和方法中的分组求和方法的应用
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目