题目内容

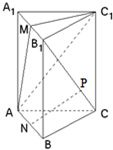11、已知直三棱柱ABC-A1B1C1中，AC=BC，M，N分别是A1B1，AB的中点，P点在线段B1C上，则NP与平面AMC1的位置关系是（　　）
分析：根据题意可得：C1M∥NC，因为C1M不在平面NCB1内，NC?平面NCB1，所以C1M∥平面NCB1．同理可得AM∥平面NCB1．可得平面C1AM∥平面NCB1．进而得到NP∥平面C1AM．
解答：解：连接B1N，
因为在直三棱柱ABC-A1B1C1中，AC=BC，M，N分别是A1B1，AB的中点，
所以C1M∥NC．
因为C1M不在平面NCB1内，NC?平面NCB1，
所以C1M∥平面NCB1．
同理可得AM∥平面NCB1．
又因为C1M∩AM=M，AM?平面C1AM，C1M?平面C1AM，
所以平面C1AM∥平面NCB1．
由因为P点在线段B1C上，所以NP∥平面C1AM．
故选B．
点评：解决此类问题的关键是熟练掌握线面平行的判断定理与面面平行的判断定理，并且结合几何体的结构特征解决线面问题．
练习册系列答案
相关题目
精英家教网如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．
（Ⅰ）求证：CF⊥BB1；
（Ⅱ）求四棱锥A-ECBB1的体积；
（Ⅲ）判断直线CF和平面AEB1的位置关系，并加以证明．
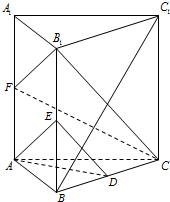已知直三棱柱ABC-A1B1C1的所有棱长都相等，且D，E，F分别为BC，BB1，AA1的中点．
（I） 求证：平面B1FC∥平面EAD；
（II）求证：BC1⊥平面EAD．
如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC，AB，AA′两两垂直，E，F，H分别是AC，AB，BC的中点，
（I）证明：EF⊥AH；    
（II）求四面体E-FAH的体积．
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
（Ⅰ）求异面直线AB和C1D所成的角（用反三角函数表示）；
（Ⅱ）若E为AB上一点，试确定点E在AB上的位置，使得A1E⊥C1D；
（Ⅲ）在（Ⅱ）的条件下，求点D到平面B1C1E的距离．
如图，已知直三棱柱ABC-A1B1C1中，AB=AC；M．N．P分别是棱BC．CC1．B1C1的中点．A1Q=3QA， BC=
2
AA1
（Ⅰ）求证：PQ∥平面ANB1；
（Ⅱ）求证：平面AMN⊥平面AMB1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网