题目内容
已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,- <Φ<
<Φ< )的图象与x轴交点为
)的图象与x轴交点为 ,相邻最高点坐标为
,相邻最高点坐标为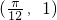 .
.
(1)求函数f(x)的表达式;
(2)求函数f(x)在[0,π]上的最值.
解:(1)∵高点坐标为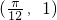 ,∴正数A=1
,∴正数A=1
∵函数图象与x轴交点为 ,相邻最高点坐标为
,相邻最高点坐标为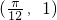 .
.
∴函数周期为T=4( +
+ )=π,可得ω=
)=π,可得ω= =2,函数表达式为f(x)=sin(2x+Φ)
=2,函数表达式为f(x)=sin(2x+Φ)
∵当x= 时,函数有最大值为1,
时,函数有最大值为1,
∴2• +φ=
+φ= +2kπ,(k∈Z),结合-
+2kπ,(k∈Z),结合- <Φ<
<Φ< ,取k=0得φ=
,取k=0得φ=
因此,函数f(x)的表达式是f(x)=sin(2x+ ).
).
(2)∵x∈[0,π],∴2x+ ∈[
∈[ ,
, ]
]
∴当x= 时,函数f(x)=sin(2×
时,函数f(x)=sin(2× +
+ )=sin
)=sin =1,达到最大值1;
=1,达到最大值1;
当x= 时,函数f(x)=sin(2×
时,函数f(x)=sin(2× +
+ )sin
)sin =-1,达到最小值-1.
=-1,达到最小值-1.
即函数f(x)在[0,π]上的最大值是f( )=1;最小值是f(
)=1;最小值是f( )=1.
)=1.
分析:(1)根据函数的最大值得到A=1,由相邻的零点与最大值的距离得到周期,进而得到ω=2,最后利用当x= 时,函数有最大值为1,求出φ=
时,函数有最大值为1,求出φ= ,得出函数f(x)的表达式;
,得出函数f(x)的表达式;
(2)根据x的范围得出2x+ 的范围,结合正弦函数的图象与性质,不难得出函数f(x)在[0,π]上的最大最小值.
的范围,结合正弦函数的图象与性质,不难得出函数f(x)在[0,π]上的最大最小值.
点评:本题给出特殊的三角函数,在已知其一个零点和最大值点情况下求函数解析式,并求它在闭区间上的最值,着重考查了三角函数的图象与性质和由y=Asin(ωx+φ)的部分图象确定其解析式等知识,属于基础题.
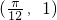 ,∴正数A=1
,∴正数A=1∵函数图象与x轴交点为
 ,相邻最高点坐标为
,相邻最高点坐标为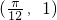 .
.∴函数周期为T=4(
 +
+ )=π,可得ω=
)=π,可得ω= =2,函数表达式为f(x)=sin(2x+Φ)
=2,函数表达式为f(x)=sin(2x+Φ)∵当x=
 时,函数有最大值为1,
时,函数有最大值为1,∴2•
 +φ=
+φ= +2kπ,(k∈Z),结合-
+2kπ,(k∈Z),结合- <Φ<
<Φ< ,取k=0得φ=
,取k=0得φ=
因此,函数f(x)的表达式是f(x)=sin(2x+
 ).
).(2)∵x∈[0,π],∴2x+
 ∈[
∈[ ,
, ]
]∴当x=
 时,函数f(x)=sin(2×
时,函数f(x)=sin(2× +
+ )=sin
)=sin =1,达到最大值1;
=1,达到最大值1;当x=
 时,函数f(x)=sin(2×
时,函数f(x)=sin(2× +
+ )sin
)sin =-1,达到最小值-1.
=-1,达到最小值-1.即函数f(x)在[0,π]上的最大值是f(
 )=1;最小值是f(
)=1;最小值是f( )=1.
)=1.分析:(1)根据函数的最大值得到A=1,由相邻的零点与最大值的距离得到周期,进而得到ω=2,最后利用当x=
 时,函数有最大值为1,求出φ=
时,函数有最大值为1,求出φ= ,得出函数f(x)的表达式;
,得出函数f(x)的表达式;(2)根据x的范围得出2x+
 的范围,结合正弦函数的图象与性质,不难得出函数f(x)在[0,π]上的最大最小值.
的范围,结合正弦函数的图象与性质,不难得出函数f(x)在[0,π]上的最大最小值.点评:本题给出特殊的三角函数,在已知其一个零点和最大值点情况下求函数解析式,并求它在闭区间上的最值,着重考查了三角函数的图象与性质和由y=Asin(ωx+φ)的部分图象确定其解析式等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目