题目内容
 已知圆C:(x+1)2+y2=8.
已知圆C:(x+1)2+y2=8.
(1)设点Q(x,y)是圆C上一点,求x+y的取值范围;
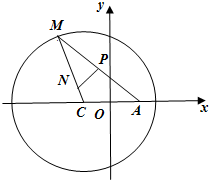
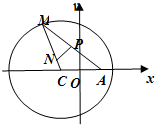
(2)如图,定点A(1,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足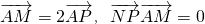 ,求点N的轨迹的内接矩形的最大面积.
,求点N的轨迹的内接矩形的最大面积.
解:(1)∵点在圆C上,
∴可设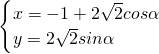 α∈[0,2π);(2分)
α∈[0,2π);(2分)
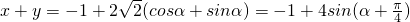 ,(4分)
,(4分)
从而x+y∈[-5,3].(6分)
(2)∵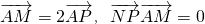 .
.
∴NP为AM的垂直平分线,
∴|NA|=|NM|.(8分)
又∵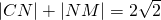 ,∴
,∴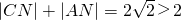 .
.
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.(10分)
且椭圆长轴长为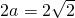 ,焦距2c=2.
,焦距2c=2.
∴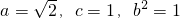 .
.
∴点N的轨迹是方程为 .(12分)
.(12分)
所以N为椭圆,其内接矩形的最大面积为 .(14分)
.(14分)
分析:(1)由已知中圆C:(x+1)2+y2=8,我们易求出圆的参数方程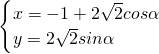 α∈[0,2π),将问题转化为三角函数值域问题,利用辅助角公式,及正弦型函数的性质,易得到答案.
α∈[0,2π),将问题转化为三角函数值域问题,利用辅助角公式,及正弦型函数的性质,易得到答案.
(2)由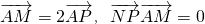 ,易得NP为AM的垂直平分线,则
,易得NP为AM的垂直平分线,则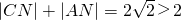 .则动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,且椭圆长轴长为
.则动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,且椭圆长轴长为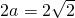 ,焦距2c=2.由此可以得到N的轨迹方程,则连接其通径四个点的内接矩形的面积最大,由此即可得到答案.
,焦距2c=2.由此可以得到N的轨迹方程,则连接其通径四个点的内接矩形的面积最大,由此即可得到答案.
点评:本题考查的知识点是圆方程的综合应用,在求x+y的取值范围时,利用参数方程可以大大简化解题的难度.

∴可设
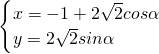 α∈[0,2π);(2分)
α∈[0,2π);(2分)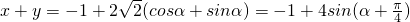 ,(4分)
,(4分)从而x+y∈[-5,3].(6分)
(2)∵
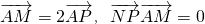 .
.∴NP为AM的垂直平分线,
∴|NA|=|NM|.(8分)
又∵
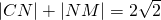 ,∴
,∴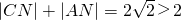 .
.∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.(10分)
且椭圆长轴长为
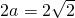 ,焦距2c=2.
,焦距2c=2.∴
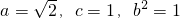 .
.∴点N的轨迹是方程为
 .(12分)
.(12分)所以N为椭圆,其内接矩形的最大面积为
 .(14分)
.(14分)分析:(1)由已知中圆C:(x+1)2+y2=8,我们易求出圆的参数方程
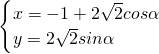 α∈[0,2π),将问题转化为三角函数值域问题,利用辅助角公式,及正弦型函数的性质,易得到答案.
α∈[0,2π),将问题转化为三角函数值域问题,利用辅助角公式,及正弦型函数的性质,易得到答案.(2)由
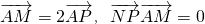 ,易得NP为AM的垂直平分线,则
,易得NP为AM的垂直平分线,则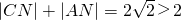 .则动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,且椭圆长轴长为
.则动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,且椭圆长轴长为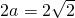 ,焦距2c=2.由此可以得到N的轨迹方程,则连接其通径四个点的内接矩形的面积最大,由此即可得到答案.
,焦距2c=2.由此可以得到N的轨迹方程,则连接其通径四个点的内接矩形的面积最大,由此即可得到答案.点评:本题考查的知识点是圆方程的综合应用,在求x+y的取值范围时,利用参数方程可以大大简化解题的难度.

练习册系列答案
相关题目