题目内容
若定义在![]() 上的函数
上的函数![]() 同时满足以下条件:①
同时满足以下条件:① ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数; ②
上是增函数; ② ![]() 是偶函数;③
是偶函数;③ ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直. (Ⅰ)求函数
垂直. (Ⅰ)求函数![]() 的解析式;(Ⅱ)设
的解析式;(Ⅱ)设![]() ,若存在
,若存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围
的取值范围
【解析】:(Ⅰ)![]() ,∵
,∵ ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() , (
, (![]() )由
)由![]() 是偶函数得:
是偶函数得:![]() ,又
,又![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,![]() ,代入(
,代入(![]() )得:
)得:![]() 即
即![]() ....5分
....5分
(Ⅱ)由已知得:若存在![]() ,使
,使![]() ,即存在
,即存在![]() ,使
,使![]() .
.
设![]() ,则
,则![]() ,.....8分
,.....8分
令![]() =0,∵
=0,∵![]() ,∴
,∴![]() , 当
, 当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() 在
在![]() 上有最大值.
上有最大值.
又![]() ,∴
,∴![]() 最小值为
最小值为![]() . 于是有
. 于是有![]() 为所求..13分
为所求..13分

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 上的函数
上的函数 同时满足:①
同时满足:① ;②
;② ;③若
;③若 ,且
,且 ,则
,则 成立.则称函数
成立.则称函数 在区间
在区间 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: 均有
均有 成立;
成立; ; ③当
; ③当 时,都有
时,都有 成立。
成立。 ,
, 的值;
的值; 的不等式
的不等式 .
. 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: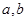 均有
均有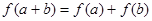 成立;
成立;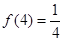
 时,都有
时,都有 成立。
成立。 ,
, 的值;
的值;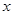 的不等式
的不等式 .
. 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: 均有
均有 成立;
成立; ;
; 时,都有
时,都有 成立。
成立。 ,
, 的值;
的值; 的不等式
的不等式 .
.