题目内容
设A,F分别是椭圆| x2 |
| a2 |
| y2 |
| b2 |
分析:由题意,椭圆上右准线上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等,根据|PF|的范围求得|FA|的范围,进而求得
的范围即离心率e的范围.
| c |
| a |
解答: 解:由题意,椭圆上右准线上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等
解:由题意,椭圆上右准线上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等
而|FA|=a+c,如图,
又|FH|=
-c
|PF|≥|FH|,
于是a+c≥
-c即ac+2c2≥a2,
∴2e2+e-1≥0,e≥
,又e∈(0,1)
故e∈[
,1)
故答案为:[
,1).
 解:由题意,椭圆上右准线上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等
解:由题意,椭圆上右准线上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等而|FA|=a+c,如图,
又|FH|=
| a2 |
| c |
|PF|≥|FH|,
于是a+c≥
| a2 |
| c |
∴2e2+e-1≥0,e≥
| 1 |
| 2 |
故e∈[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题考查线段的中点公式,两直线垂直的性质,以及椭圆的简单性质的应用.属于基础题.

练习册系列答案
相关题目
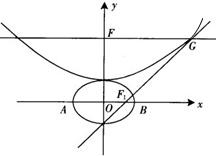 设b>0,椭圆方程为
设b>0,椭圆方程为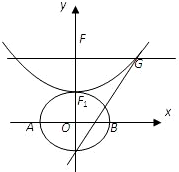 设b>0,椭圆方程为
设b>0,椭圆方程为 设b>0,椭圆方程为
设b>0,椭圆方程为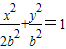 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.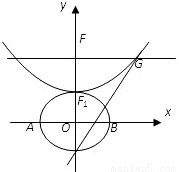 设b>0,椭圆方程为
设b>0,椭圆方程为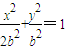 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1. 设b>0,椭圆方程为
设b>0,椭圆方程为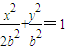 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.