题目内容
已知正方体ABCD-A1B1C1D1的棱长为1,动点P在正方体ABCD-A1B1C1D1表面上运动,且PA=r(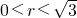 ),记点P的轨迹的长度为f(r),则
),记点P的轨迹的长度为f(r),则 =________.(填上所有可能的值).
=________.(填上所有可能的值).
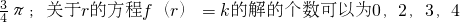
分析:由题意画出图形并得出相应的解析式,画出其图象,经过讨论即可得出答案.
解答:如图所示:①当0<r≤1时,f(r)=3×
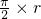 =
=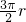 ;∴
;∴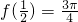 .此时,由一次函数的单调性可得:
.此时,由一次函数的单调性可得: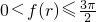 <5.
<5.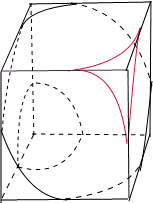
②当1<r≤
 时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则
时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则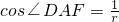 ,
,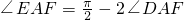 ,
,∴cos∠EAF=sin2∠DAF=2×
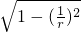 ×
×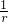 =
=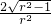 ,cos∠EAG=
,cos∠EAG=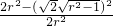 =
= ,
,∴f(r)=3r
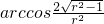 +3r
+3r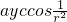 ;
;③当
 时,∵CM=
时,∵CM= ,∴
,∴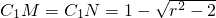 ,∴cos∠MAN=
,∴cos∠MAN=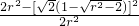 =
=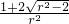 ,
,∴f(r)=3r
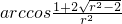 .
.综上可知:当0<r≤1时,
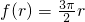 ;当1<r≤
;当1<r≤ 时,f(r)=3r
时,f(r)=3r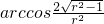 +3r
+3r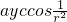 ;当
;当 时,∴f(r)=3r
时,∴f(r)=3r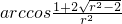 .
.根据以上解析式及图性和对称性可得f(r)的图象:
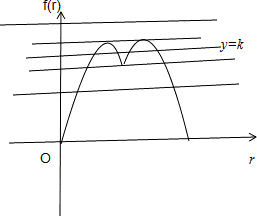
由图象不难看出:函数y=f(r)与y=k的交点个数分别为,0,2,3,4.
故答案为
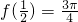 .关于r的方程f(r)=k的解的个数可能为0,2,3,4.
.关于r的方程f(r)=k的解的个数可能为0,2,3,4.点评:熟练掌握数形结合、分类讨论的思想方法、数形结合的思想方法是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.