题目内容
若椭圆b2x2+a2y2=a2b2(a>b>0)的左焦点为F,右顶点为A,上顶点为B,且离心率为 ,求∠ABF.
,求∠ABF.
 ,求∠ABF.
,求∠ABF.
∠ABF=90°.
椭圆方程为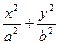 =1(a>b>0),
=1(a>b>0),
则F(-c,0)、A(a,0)、B(0,b),
|AB|= ,|AF|=a+c,|BF|=a.
,|AF|=a+c,|BF|=a.
∴cos∠ABF=
 .
.
∵e= =
= ,∴a2-ac-c2=0.
,∴a2-ac-c2=0.
∴cos∠ABF=0.
∴∠ABF=90°.
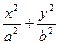 =1(a>b>0),
=1(a>b>0),则F(-c,0)、A(a,0)、B(0,b),
|AB|=
 ,|AF|=a+c,|BF|=a.
,|AF|=a+c,|BF|=a.∴cos∠ABF=

 .
.∵e=
 =
= ,∴a2-ac-c2=0.
,∴a2-ac-c2=0.∴cos∠ABF=0.
∴∠ABF=90°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
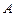 到两个定点
到两个定点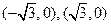 的距离的和等于4.
的距离的和等于4.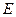 的方程;
的方程;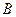 在曲线
在曲线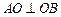 ,试求
,试求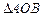 面积的最大值和最小值.
面积的最大值和最小值. +
+ =1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.
=1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.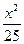 +
+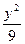 =1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1上一点P到两焦点距离之积为m,则m最大时求P点坐标. =1的右焦点为F,设A(-
=1的右焦点为F,设A(- ,3),P是椭圆上一动点,则|AP|+5|PF|取最小值时,P的坐标为( )
,3),P是椭圆上一动点,则|AP|+5|PF|取最小值时,P的坐标为( ) +
+ =1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
=1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________. 所表示的曲线是( )
所表示的曲线是( ) +
+  =1(x≠±2)
=1(x≠±2) +
+ =1(y≠±2)
=1(y≠±2)


 ,求△AOB面积的最大值
,求△AOB面积的最大值