题目内容
已知函数 ,f(0)=1-
,f(0)=1- ,且
,且
(1)求a,b的值及f(x)的最大值和最小值;
(2)若不等式|f(x)-m|<2在x 上恒成立,求实数m的取值范围;
上恒成立,求实数m的取值范围;
(3)由f(x)的图象是否可以经过平移变换得到一个奇函数y=g(x)的图象?若能,请写出你的变换过程;否则说明理由.
解:(1) =a
=a 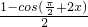 +bcos2x=
+bcos2x= +
+ +bcos2x.
+bcos2x.
由f(0)=1- ,且
,且 可得
可得 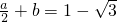 ,且
,且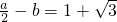 ,∴a=2,b=-
,∴a=2,b=- .
.
∴f(x)=1+sin2x- cos2x=1+2sin(2x-
cos2x=1+2sin(2x- ),故它的最大值为3,最小值等于-1.
),故它的最大值为3,最小值等于-1.
(2)若不等式|f(x)-m|<2在x 上恒成立,即m-3<2sin(2x-
上恒成立,即m-3<2sin(2x- )<1+m.
)<1+m.
由于 ≤x≤
≤x≤ ,∴
,∴ ≤2x-
≤2x- ≤
≤ ,∴
,∴ ≤2sin(2x-
≤2sin(2x- )≤2.
)≤2.
∴1+m>2,m-3< ,解得1<m<
,解得1<m< ,
,
故实数m的取值范围(1, ).
).
(3)由f(x)=1+2sin(2x- )可得,
)可得,
把f(x)的图象向左平移 个单位得到y=1+2sin2x的图象,
个单位得到y=1+2sin2x的图象,
再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,
故由f(x)的图象可以经过平移变换得到一个奇函数y=g(x)的图象.
分析:(1)利用三角函数的恒等变换化简f(x)的解析式,由条件求出a、b的值,进一步化简f(x)=1+2sin(2x- ),从而求出函数的最大值和最小值.
),从而求出函数的最大值和最小值.
(2)由条件可得x 上时,m-3<2sin(2x-
上时,m-3<2sin(2x- )<1+m恒成立,故有
)<1+m恒成立,故有  ≤2sin(2x-
≤2sin(2x- )≤2.由 1+m>2,m-3<
)≤2.由 1+m>2,m-3< ,求出实数m的取值范围.
,求出实数m的取值范围.
(3)由f(x)=1+2sin(2x- ) 可得,把f(x)的图象向左平移
) 可得,把f(x)的图象向左平移 个单位得到y=1+2sin2x的图象,再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,从而得到结论.
个单位得到y=1+2sin2x的图象,再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,从而得到结论.
点评:本题主要考查三角函数的恒等变换,三角函数y=Asin(ωx+∅)的图象变换,正弦函数的值域,函数的恒成立问题,以及函数的奇偶性,属于中档题.
 =a
=a 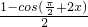 +bcos2x=
+bcos2x= +
+ +bcos2x.
+bcos2x.由f(0)=1-
 ,且
,且 可得
可得 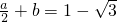 ,且
,且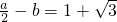 ,∴a=2,b=-
,∴a=2,b=- .
.∴f(x)=1+sin2x-
 cos2x=1+2sin(2x-
cos2x=1+2sin(2x- ),故它的最大值为3,最小值等于-1.
),故它的最大值为3,最小值等于-1.(2)若不等式|f(x)-m|<2在x
 上恒成立,即m-3<2sin(2x-
上恒成立,即m-3<2sin(2x- )<1+m.
)<1+m.由于
 ≤x≤
≤x≤ ,∴
,∴ ≤2x-
≤2x- ≤
≤ ,∴
,∴ ≤2sin(2x-
≤2sin(2x- )≤2.
)≤2.∴1+m>2,m-3<
 ,解得1<m<
,解得1<m< ,
,故实数m的取值范围(1,
 ).
).(3)由f(x)=1+2sin(2x-
 )可得,
)可得,把f(x)的图象向左平移
 个单位得到y=1+2sin2x的图象,
个单位得到y=1+2sin2x的图象,再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,
故由f(x)的图象可以经过平移变换得到一个奇函数y=g(x)的图象.
分析:(1)利用三角函数的恒等变换化简f(x)的解析式,由条件求出a、b的值,进一步化简f(x)=1+2sin(2x-
 ),从而求出函数的最大值和最小值.
),从而求出函数的最大值和最小值.(2)由条件可得x
 上时,m-3<2sin(2x-
上时,m-3<2sin(2x- )<1+m恒成立,故有
)<1+m恒成立,故有  ≤2sin(2x-
≤2sin(2x- )≤2.由 1+m>2,m-3<
)≤2.由 1+m>2,m-3< ,求出实数m的取值范围.
,求出实数m的取值范围.(3)由f(x)=1+2sin(2x-
 ) 可得,把f(x)的图象向左平移
) 可得,把f(x)的图象向左平移 个单位得到y=1+2sin2x的图象,再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,从而得到结论.
个单位得到y=1+2sin2x的图象,再向下平移1个单位可得y=2sin2x的图象,而y=2sin2x就是奇函数,从而得到结论.点评:本题主要考查三角函数的恒等变换,三角函数y=Asin(ωx+∅)的图象变换,正弦函数的值域,函数的恒成立问题,以及函数的奇偶性,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知函数,f(x)=
,则复合函数f{f[f(-1)]}=( )
|
| A、x2+1 |
| B、π2+1 |
| C、-π |
| D、0 |
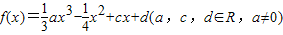 满足f(0)=0,f′(1)=0,且f(x)在R上单调递增.
满足f(0)=0,f′(1)=0,且f(x)在R上单调递增.