Question

已知函数f(x)=|lnx|-(

1

2

)x有两个零点x₁，x₂，则有（　　）

A．x₁x₂=1

B．x₁x₂＜x₁+x₂

C．x₁x₂=x₁+x₂

D．x₁x₂＞x₁+x₂

Answer 1

分析：先利用图象法确定两个零点x₁，x₂的取值范围，然后利用指数函数的性质进行判断．

解答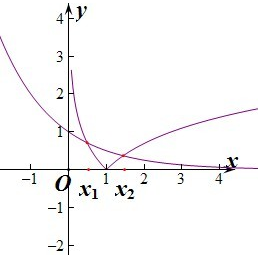：解：令f(x)=|lnx|-(

1

2

)x=0，得|lnx|=(

1

2

)x，设函数分别为y=|lnx|，y=(

1

2

)x，
分别在同一坐标系中，作出函数为y=|lnx|，y=(

1

2

)x的图象，
由图象知函数的两个零点一个大于1，一个小于1，不妨设x₁＜x₂，则0＜x₁＜1，x₂＞1．
即|lnx1|=(

1

2

)x1=-lnx1，①，
|lnx2|=(

1

2

)x2=lnx2  ②
②-①得lnx1x2=(

1

2

)x2-(

1

2

)x1，因为函数y=(

1

2

)x是减函数，
所以(

1

2

)x2-(

1

2

)x1＜0，即lnx₁x₂＜0，所以0＜x₁x₂＜1．
所以x₁x₂＜x₁+x₂．
故选B．

点评：本题考查函数零点的应用以及指数函数和对数函数的性质，综合性较强，使用数形结合思想是解决好本题的关键．