题目内容
已知函数f(x)的定义域是 ,且f(x)+f(2-x)=0,
,且f(x)+f(2-x)=0,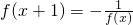 ,当
,当 时,f(x)=3x.
时,f(x)=3x.
(1)求证:f(x+2)=f(x)且f(x)是奇函数;
(2)求当 时函数f(x)的解析式,并求x∈
时函数f(x)的解析式,并求x∈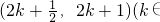 Z)时f(x)的解析式;
Z)时f(x)的解析式;
(3)当x∈ 时,解不等式log3f(x)>x2-(2k+2)x+2k+1.
时,解不等式log3f(x)>x2-(2k+2)x+2k+1.
解:(1)由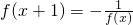 得
得 ,
,
由f(x)+f(2-x)=0得f(x)+f(-x)=0,
故f(x)是奇函数.
(2)当x∈ 时,
时, ,
,
∴f(1-x)=31-x.
而 ,
,
∴f(x)=3x-1.
当x∈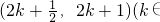 Z)时,
Z)时, ,
,
∴f(x-2k)=3x-2k-1,
因此f(x)=f(x-2k)=3x-2k-1.
(3)不等式log3f(x)>x2-(2k+2)x+2k+1
即为x-2k-1>x2-(2k+2)x+2k+1,
即x2-(2k+3)x+2(2k+1)<0,(x-2)[x-(2k+1)]<0
当2k+1<2即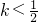 时,x∈(2k+1,2)与条件不符;
时,x∈(2k+1,2)与条件不符;
当2k+1=2即 时,无解.
时,无解.
当2k+1>2即 时,若
时,若 即
即 时整数k不存在;
时整数k不存在;
若 即
即 时,
时, .
.
综上:k≥1时 ,k<1时x∈φ
,k<1时x∈φ
分析:(1)根据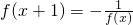 与f(x+2)=f(x)可求出f(x)与f(-x)的关系,从而确定函数的奇偶性;
与f(x+2)=f(x)可求出f(x)与f(-x)的关系,从而确定函数的奇偶性;
(2)当x∈ 时,
时, ,代入已知解析式,从而求出所求,当x∈
,代入已知解析式,从而求出所求,当x∈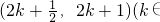 Z)时,
Z)时, ,代入已知解析式即可求出所求;
,代入已知解析式即可求出所求;
(3)将函数解析式代入,然后讨论两根的大小,从而求出不等式的解集.
点评:本题主要考查了抽象函数及其应用,以及在给定区间上的解析式和不等式的解集等有关问题,属于中档题.
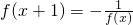 得
得 ,
,由f(x)+f(2-x)=0得f(x)+f(-x)=0,
故f(x)是奇函数.
(2)当x∈
 时,
时, ,
,∴f(1-x)=31-x.
而
 ,
,∴f(x)=3x-1.
当x∈
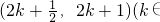 Z)时,
Z)时, ,
,∴f(x-2k)=3x-2k-1,
因此f(x)=f(x-2k)=3x-2k-1.
(3)不等式log3f(x)>x2-(2k+2)x+2k+1
即为x-2k-1>x2-(2k+2)x+2k+1,
即x2-(2k+3)x+2(2k+1)<0,(x-2)[x-(2k+1)]<0
当2k+1<2即
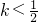 时,x∈(2k+1,2)与条件不符;
时,x∈(2k+1,2)与条件不符; 当2k+1=2即
 时,无解.
时,无解. 当2k+1>2即
 时,若
时,若 即
即 时整数k不存在;
时整数k不存在;若
 即
即 时,
时, .
. 综上:k≥1时
 ,k<1时x∈φ
,k<1时x∈φ分析:(1)根据
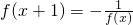 与f(x+2)=f(x)可求出f(x)与f(-x)的关系,从而确定函数的奇偶性;
与f(x+2)=f(x)可求出f(x)与f(-x)的关系,从而确定函数的奇偶性;(2)当x∈
 时,
时, ,代入已知解析式,从而求出所求,当x∈
,代入已知解析式,从而求出所求,当x∈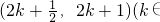 Z)时,
Z)时, ,代入已知解析式即可求出所求;
,代入已知解析式即可求出所求;(3)将函数解析式代入,然后讨论两根的大小,从而求出不等式的解集.
点评:本题主要考查了抽象函数及其应用,以及在给定区间上的解析式和不等式的解集等有关问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
