题目内容
已知函数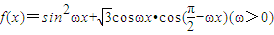 ,且函数y=f(x)的图象相邻两条对称轴之间的距离为
,且函数y=f(x)的图象相邻两条对称轴之间的距离为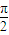 .
.(Ⅰ)求ω的值及f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若
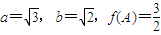 ,求角C.
,求角C.
【答案】分析:(Ⅰ)把函数解析式第一项利用二倍角的余弦函数公式化简,第二项第二个因式利用诱导公式化简后,利用二倍角的正弦函数公式化简,整理后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据相邻对称轴间的距离求出函数周期,利用周期公式即可求出ω的值,由正弦函数的单调递增区间[2kπ-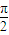 ,2kπ+
,2kπ+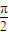 ]即可得到函数的单调递增区间;
]即可得到函数的单调递增区间;
(Ⅱ)把x=A代入第一问化简后的函数解析式,令其值等于 ,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.
,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.
解答:解:(Ⅰ)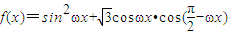
=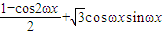
=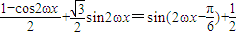 ,
,
∵函数y=f(x)的图象相邻两条对称轴之间的距离为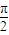 ,
,
∴T=π,∴ω=1…(5分)
∵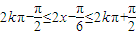 ,∴
,∴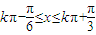 ,
,
则y=f(x)的单调递增区间为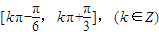 ;…(7分)
;…(7分)
(Ⅱ)∵ ,∴
,∴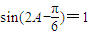 ,
,
∵0<A<π,∴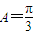 ,…(10分)
,…(10分)
∵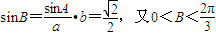 ,
,
∴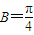 ,
,
∴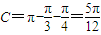 .…(14分)
.…(14分)
点评:此题属于解三角形的题型,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,正弦函数的单调性,正弦定理,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.
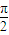 ,2kπ+
,2kπ+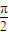 ]即可得到函数的单调递增区间;
]即可得到函数的单调递增区间;(Ⅱ)把x=A代入第一问化简后的函数解析式,令其值等于
 ,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.
,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.解答:解:(Ⅰ)
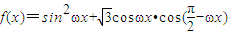
=
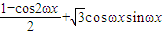
=
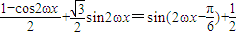 ,
,∵函数y=f(x)的图象相邻两条对称轴之间的距离为
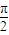 ,
,∴T=π,∴ω=1…(5分)
∵
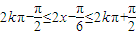 ,∴
,∴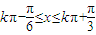 ,
,则y=f(x)的单调递增区间为
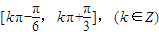 ;…(7分)
;…(7分)(Ⅱ)∵
 ,∴
,∴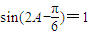 ,
,∵0<A<π,∴
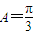 ,…(10分)
,…(10分)∵
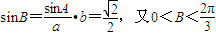 ,
,∴
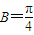 ,
,∴
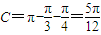 .…(14分)
.…(14分)点评:此题属于解三角形的题型,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,正弦函数的单调性,正弦定理,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
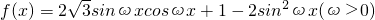 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.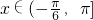 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间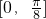 上的最小值.
上的最小值.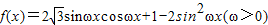 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.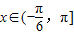 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移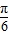 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间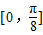 上的最小值.
上的最小值. ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π. ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值. ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.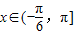 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.