题目内容
 如图,在梯形ABCD中,AD∥BC,AD⊥AB,AD=1,AB=2,BC=3,P是BC上的一个动点,当
如图,在梯形ABCD中,AD∥BC,AD⊥AB,AD=1,AB=2,BC=3,P是BC上的一个动点,当 取最小值时,tan∠DPA的值是
取最小值时,tan∠DPA的值是
- A.

- B.
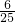
- C.

- D.

D
分析:由余弦定理可得 1=AP2+DP2-2 ,即
,即  =
= ,利用基本不等式可得当
,利用基本不等式可得当 最小时,点P是AD的中垂线和BC的交点,tan
最小时,点P是AD的中垂线和BC的交点,tan  =
= =
= ,利用倍角的正切公式求得tan∠APD 的值.
,利用倍角的正切公式求得tan∠APD 的值.
解答:∵ =PD•PA cos∠APD,
=PD•PA cos∠APD,
△PDA中,由余弦定理可得
1=AP2+DP2-2AP•DPcos∠APD=AP2+DP2-2 ,
,
∴ =
= ≥
≥ ,当且仅当AP=DP 时,等号成立.
,当且仅当AP=DP 时,等号成立.
故当 最小时,点P是AD的中垂线和BC的交点,tan
最小时,点P是AD的中垂线和BC的交点,tan  =
= =
= ,
,
∴tan∠APD= =
= =
= ,
,
故选 D.
点评:本题考查余弦定理,基本不等式,二倍角的正切公式的应用,求出tan 的值,是解题的关键,属于中档题.
的值,是解题的关键,属于中档题.
分析:由余弦定理可得 1=AP2+DP2-2
 ,即
,即  =
= ,利用基本不等式可得当
,利用基本不等式可得当 最小时,点P是AD的中垂线和BC的交点,tan
最小时,点P是AD的中垂线和BC的交点,tan  =
= =
= ,利用倍角的正切公式求得tan∠APD 的值.
,利用倍角的正切公式求得tan∠APD 的值.解答:∵
 =PD•PA cos∠APD,
=PD•PA cos∠APD,△PDA中,由余弦定理可得
1=AP2+DP2-2AP•DPcos∠APD=AP2+DP2-2
 ,
,∴
 =
= ≥
≥ ,当且仅当AP=DP 时,等号成立.
,当且仅当AP=DP 时,等号成立.故当
 最小时,点P是AD的中垂线和BC的交点,tan
最小时,点P是AD的中垂线和BC的交点,tan  =
= =
= ,
,∴tan∠APD=
 =
= =
= ,
,故选 D.
点评:本题考查余弦定理,基本不等式,二倍角的正切公式的应用,求出tan
 的值,是解题的关键,属于中档题.
的值,是解题的关键,属于中档题. 
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
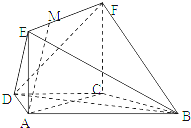 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.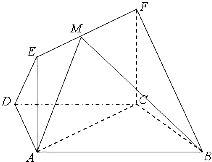 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.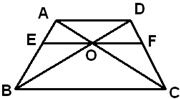 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.