Question

如图,已知α∥β，异面直线AB、CD和平面α、β分别交于A、B、C、D四点，E、F、G、H分别是AB、BC、CD、DA的中点.

求证：(1)E、F、G、H共面；

(2)面EFGH∥平面α.

Answer 1

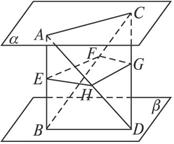
思路点拨：要证明四点共面,结合已知条件可以转而证明其中一对直线平行;要证明面面平行,容易想到利用面面平行的判定定理来考虑,利用已知的面面平行条件,从而将问题解决.

证明：1)∵E、H分别是AB、DA的中点，

∴EH∥BD且EH=BD.

同理，FG∥BD且FG=BD，

∴FG∥EH且FG=EH.∴四边形EFGH是平行四边形，即E、F、G、H共面.

(2)平面ABD和平面α有一个公共点A，设两平面交于过点A的直线AD′.

∵α∥β，∴AD′∥BD.

又∵BD∥EH,∴EH∥BD∥AD′.

∴EH∥平面α，EH∥平面β.

同理，EF∥平面α，EF∥平面β.

∴平面EFGH∥平面α∥平面β.