题目内容
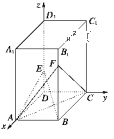
【题目】如图，在正四棱柱
中，已知AB＝2，
，
E、F分别为
、
上的点，且
.
(1)求证：BE⊥平面ACF；
(2)求点E到平面ACF的距离．
【答案】（1）见解析（2）
【解析】
分析：（1）以
为原点，
所在直线分别为
轴建立空间直角坐标系，写出要用的点的坐标，要证明线与面垂直，只需证明这条直线与平面上的两条直线垂直即可；（2）
为平面
的一个法向量，向量
在上的射影长即为
到平面的距离，根据点到面的距离公式可得到结论.
详解：(1)证明：以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立如图所示空间直角坐标系，则D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、D1(0,0,5)、E(0,0,1)、F(2,2,4)．
∴
＝(－2,2,0)、
＝(0,2,4)、
＝(－2，－2,1)、
＝(－2，0,1)．
∵·＝0，·＝0，
∴BE⊥AC，BE⊥AF，且AC∩AF＝A.
∴BE⊥平面ACF.
(2)由(1)知，为平面ACF的一个法向量，
∴点E到平面ACF的距离d＝
＝
.
故点E到平面ACF的距离为.
练习册系列答案
相关题目
