题目内容
以椭圆的两个焦点为直径的端点的圆与椭圆交于四个不同的点,顺次连接这四个点和两个焦点恰好组成一个正六边形,那么这个椭圆的离心率为
- A.
 -
-
- B.
 -1
-1 - C.

- D.

B
分析:设椭圆的两个焦点为F1,F2,圆与椭圆交于A,B,C,D四个不同的点,设|F1F2|=2c,则|DF1|=c,|DF2|= c.由椭圆的定义知2a=||DF1|+|DF2|=
c.由椭圆的定义知2a=||DF1|+|DF2|= c+c,根据离心率公式求得答案.
c+c,根据离心率公式求得答案.
解答:设椭圆的两个焦点为F1,F2,圆与椭圆交于A,B,C,D四个不同的点,
设|F1F2|=2c,则|DF1|=c,|DF2|= c.
c.
椭圆定义,得2a=||DF1|+|DF2|= c+c,
c+c,
所以e= =
=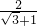 =
= -1,
-1,
故选B.
点评:本题主要考查了椭圆的简单性质.特别是椭圆定义的应用.
分析:设椭圆的两个焦点为F1,F2,圆与椭圆交于A,B,C,D四个不同的点,设|F1F2|=2c,则|DF1|=c,|DF2|=
 c.由椭圆的定义知2a=||DF1|+|DF2|=
c.由椭圆的定义知2a=||DF1|+|DF2|= c+c,根据离心率公式求得答案.
c+c,根据离心率公式求得答案.解答:设椭圆的两个焦点为F1,F2,圆与椭圆交于A,B,C,D四个不同的点,
设|F1F2|=2c,则|DF1|=c,|DF2|=
 c.
c.椭圆定义,得2a=||DF1|+|DF2|=
 c+c,
c+c,所以e=
 =
=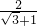 =
= -1,
-1,故选B.
点评:本题主要考查了椭圆的简单性质.特别是椭圆定义的应用.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,直线
,直线 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点
,右焦点 ,直线
,直线 过点
过点 垂
垂 ,线段
,线段 垂直平分线交
垂直平分线交 ,求点
,求点 的方程;
的方程; 轴上时,在曲线
轴上时,在曲线