题目内容
给出下列四个命题:
①若|x-lgx|<x+|lgx|成立,则x>1;
②抛物线y=2x2的焦点坐标是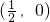 ;
;
③已知 ,
, 与
与 的夹角为
的夹角为 ,则
,则 在
在 上的投影为3;
上的投影为3;
④已知f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则
处取得最小值,则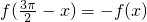 ;.
;.
其中正确命题的序号是________.
①③④
分析:依次分析命题:当0<x≤1时,|x-lgx|=x+|lgx|;当x>1时,|x-lgx|<x+|lgx|,故①成立;抛物线y=2x2的焦点坐标是(0, ),②不成立;
),②不成立; 在
在 上的投影=|
上的投影=| |+
|+ =2+2×
=2+2× =3,③成立;f(x)=asinx-bcosx,(a,b∈R)在
=3,③成立;f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则
处取得最小值,则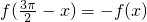 ,④成立,综合可得答案.
,④成立,综合可得答案.
解答:当0<x<1时,|x-lgx|=x+|lgx|;
当x=1时,|x-lgx|=x+|lgx|;
当x>1时,|x-lgx|<x+|lgx|.
∴若|x-lgx|<x+|lgx|成立,则x>1,即①成立;
∵抛物线y=2x2的焦点坐标是(0, ),∴②不成立;
),∴②不成立;
 在
在 上的投影=|
上的投影=| |+
|+ =2+2×
=2+2× =3,∴③成立;
=3,∴③成立;
f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则
处取得最小值,则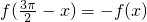 ,即④成立.
,即④成立.
故答案为:①③④.
点评:本题考查命题的真假判断与应用,解题时要注意抛物线的性质、向量的性质和绝对值不等式的应用.
分析:依次分析命题:当0<x≤1时,|x-lgx|=x+|lgx|;当x>1时,|x-lgx|<x+|lgx|,故①成立;抛物线y=2x2的焦点坐标是(0,
 ),②不成立;
),②不成立; 在
在 上的投影=|
上的投影=| |+
|+ =2+2×
=2+2× =3,③成立;f(x)=asinx-bcosx,(a,b∈R)在
=3,③成立;f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则
处取得最小值,则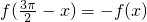 ,④成立,综合可得答案.
,④成立,综合可得答案.解答:当0<x<1时,|x-lgx|=x+|lgx|;
当x=1时,|x-lgx|=x+|lgx|;
当x>1时,|x-lgx|<x+|lgx|.
∴若|x-lgx|<x+|lgx|成立,则x>1,即①成立;
∵抛物线y=2x2的焦点坐标是(0,
 ),∴②不成立;
),∴②不成立; 在
在 上的投影=|
上的投影=| |+
|+ =2+2×
=2+2× =3,∴③成立;
=3,∴③成立;f(x)=asinx-bcosx,(a,b∈R)在
 处取得最小值,则
处取得最小值,则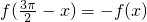 ,即④成立.
,即④成立.故答案为:①③④.
点评:本题考查命题的真假判断与应用,解题时要注意抛物线的性质、向量的性质和绝对值不等式的应用.

练习册系列答案
相关题目