题目内容
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛:答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为| 1 | 9 |
(1)求选手甲可进入决赛的概率;
(2)设选手甲在初赛中答题的个数为ξ,试求ξ的分布列,并求ξ的数学期望.
分析:(1)设选手甲任答一题,正确的概率为p,根据甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为
,列出关于P的方程,得到甲答对题目的概率,选手甲能够进入决赛包括两种情况,这两种情况是互斥的,由互斥事件的概率公式计算得到答案.
(2)由题意知ξ可取3,4,5,结合变量对应的事件和独立重复试验的概率公式写出变量的概率,最后一个变量的概率可以用1减去其余变量的概率得到,写出分布列做出期望.
| 1 |
| 9 |
(2)由题意知ξ可取3,4,5,结合变量对应的事件和独立重复试验的概率公式写出变量的概率,最后一个变量的概率可以用1减去其余变量的概率得到,写出分布列做出期望.
解答:解:(1)设选手甲任答一题,正确的概率为p,
依题意(1-p)2=
,p=
,
甲选答3道题目后进入决赛的概率为(
)3=
,
甲选答4道、5道题目后进入决赛的概率分别为
(
)3•
=
,
(
)3(
)2=
,
∴选手甲可进入决赛的概率P=
+
+
=
.
(2)由题意知ξ可取3,4,5,
依题意P(ξ=3)=
+
=
,
P(ξ=4)=
(
)2•
•
+
(
)2•
•
=
,P(ξ=5)=
(
)2•(
)2•
+
(
)2•(
)2•
=
∴ξ的分布列为:
∴Eξ=3×
+4×
+5×
=
.
依题意(1-p)2=
| 1 |
| 9 |
| 2 |
| 3 |
甲选答3道题目后进入决赛的概率为(
| 2 |
| 3 |
| 8 |
| 27 |
甲选答4道、5道题目后进入决赛的概率分别为
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
∴选手甲可进入决赛的概率P=
| 8 |
| 27 |
| 8 |
| 27 |
| 16 |
| 81 |
| 64 |
| 81 |
(2)由题意知ξ可取3,4,5,
依题意P(ξ=3)=
| 8 |
| 27 |
| 1 |
| 27 |
| 1 |
| 3 |
P(ξ=4)=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
∴ξ的分布列为:
| ξ | 3 | 4 | 5 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
点评:本题考查等可能事件的概率,考查离散型随机变量的分布列和期望,考查独立重复试验的概率公式,本题是一个综合题目,考查的知识点比较全面,在应用独立重复试验的概率公式时,注意数字运算不要出错.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
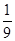 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为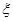 ,试写出
,试写出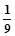 (已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(已知甲回答每个问题的正确率相同,并且相互之间没有影响) 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对 题或答错
题或答错 .
. ,试求
,试求