题目内容
定义在R上的函数f(x) 满足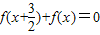 且
且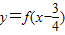 为奇函数.
为奇函数.给出下列命题:
(1)函数f(x) 的最小正周期为
 ;
;(2)函数y=f(x) 的图象关于点
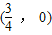 对称;
对称;(3)函数y=f(x) 的图象关于y 轴对称.其中真命题有 .(填序号)
【答案】分析:本题可先由恒等式 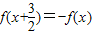 得出函数的周期是3,可以判断(1),再由函数
得出函数的周期是3,可以判断(1),再由函数 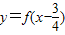 是奇函数求出函数的对称点来判断(2)(3),综合可得答案.
是奇函数求出函数的对称点来判断(2)(3),综合可得答案.
解答:解:由题意定义在R上的函数y=f(x)满足条件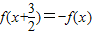 ,
,
故有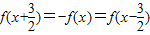 恒成立,故函数周期是3,
恒成立,故函数周期是3,
故(1)错;
又函数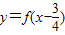 是奇函数,
是奇函数,
故函数y=f(x)的图象关于点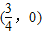 对称,
对称,
由此知(2)(3)是正确的选项,
故答案为:(2)(3)
点评:本题考查奇偶函数图象的对称性,求解本题的关键是由题设条件把函数的性质研究清楚,解答关键是得出函数是周期函数.
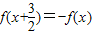 得出函数的周期是3,可以判断(1),再由函数
得出函数的周期是3,可以判断(1),再由函数 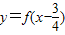 是奇函数求出函数的对称点来判断(2)(3),综合可得答案.
是奇函数求出函数的对称点来判断(2)(3),综合可得答案.解答:解:由题意定义在R上的函数y=f(x)满足条件
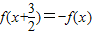 ,
,故有
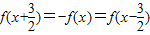 恒成立,故函数周期是3,
恒成立,故函数周期是3,故(1)错;
又函数
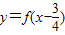 是奇函数,
是奇函数,故函数y=f(x)的图象关于点
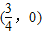 对称,
对称,由此知(2)(3)是正确的选项,
故答案为:(2)(3)
点评:本题考查奇偶函数图象的对称性,求解本题的关键是由题设条件把函数的性质研究清楚,解答关键是得出函数是周期函数.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目