Question

已知函数f(x)=(|x|-b)²+c，函数g(x)=x+m，

(1)当b=2，m=-4时，f(x)g(x)恒成立，求实数c的取值范围；

(2)当c=-3，m=-2时，方程f(x)=g(x)有四个不同的解，求实数b的取值范围.

Answer 1

（1）c??–（2）1<b<

解析:

(1)c??x–4–(|x|–2)²=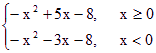，由图象得.

    (2)(|x|–b)²–3=x–2，即(|x|–b)²=x+1有四个不同的解，

     ∴ (x–b)²=x+1(x??0)有两个不同解以及(x+b)²=x+1(x<0)也有两个不同解，

     由根的分布得b??1且1<b<，∴1<b<.