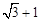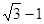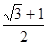题目内容
设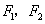 分别是双曲线
分别是双曲线 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点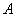 ,使
,使 且
且 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B. | C.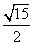 | D. |
B
解析

练习册系列答案
相关题目
已知椭圆的离心率为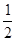 ,焦点是
,焦点是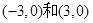 ,则椭圆方程为 ( ■ )
,则椭圆方程为 ( ■ )
A.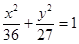 | B.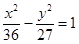 | C.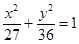 | D.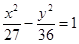 |
已知椭圆C: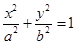
 的离心率为
的离心率为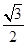 ,过右焦点
,过右焦点 且斜率为
且斜率为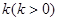 的直线与椭圆C相交于
的直线与椭圆C相交于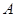 、
、 两点.若
两点.若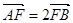 ,则
,则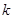 =( )
=( )
A. | B.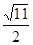 | C.2 | D. |
已知双曲线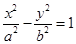 的一条渐近线方程为
的一条渐近线方程为 ,则该双曲线的离心率为
,则该双曲线的离心率为
A.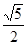 | B.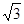 | C.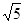 | D.2 |
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程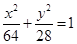 ,点
,点 是它的两个焦点.当静止的小球从点
是它的两个焦点.当静止的小球从点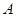 开始出发,沿直线运动,经椭圆壁反射后再回到点
开始出发,沿直线运动,经椭圆壁反射后再回到点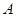 时,此时小球经过的路程可能是 ( )
时,此时小球经过的路程可能是 ( )
A.32或4或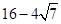 | B.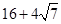 或28或 或28或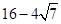 |
C.28或4或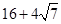 | D.32或28或4 |
过点P(2,-2)且与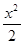 - y 2=1有相同渐近线的双曲线方程是 ( )
- y 2=1有相同渐近线的双曲线方程是 ( )
A. | B.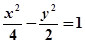 | C. | D.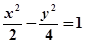 |
椭圆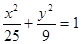 上一点M到焦点
上一点M到焦点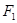 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则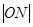 等于( )
等于( )
| A.2 | B.4 | C.6 | D. |
若直线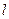 过点
过点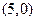 与双曲线
与双曲线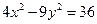
 只有一个公共点,则这样的直线有
只有一个公共点,则这样的直线有
| A.0条 | B.1条 | C.2条 | D.4条 |