题目内容
在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.

证明:(Ⅰ)在四棱锥![]() 中,因为
中,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() . 因为
. 因为![]() , 所以
, 所以![]() .
.
因为![]() , 所以
, 所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅱ) 如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() . 不妨设
. 不妨设![]() ,则
,则![]() .
.
则![]() .
.
 所以
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() .
.
所以 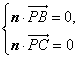 .即
.即![]() .
.
令![]() ,则
,则![]() .
.
所以![]() 所以
所以![]()
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)(法一)当![]() 为线段
为线段![]() 的中点时,
的中点时,![]() 平面
平面![]() .
.
如图:分别取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
所以![]() ,且
,且![]() . 因为
. 因为![]() 且
且![]() ,
,
所以![]() 且
且![]() . 所以四边形
. 所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() . 因为
. 因为![]() , 所以三角形
, 所以三角形![]() 是等腰三角形.
是等腰三角形.
所以![]() . 因为
. 因为![]() 平面
平面![]() , 所以
, 所以![]() .
.
因为![]() , 所以
, 所以![]() 平面
平面![]() . 所以
. 所以![]() 平面
平面![]() .
.
即在线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.
(法二)设在线段![]() 上存在点
上存在点![]() ,当
,当![]() 时,
时,![]() 平面
平面![]() .
.
设![]() ,则
,则![]() .所以
.所以![]() .
.
即![]() .所以
.所以![]() .
.
所以![]() .由(Ⅱ)可知平面
.由(Ⅱ)可知平面![]() 的法向量
的法向量![]() .
.
若![]() 平面
平面![]() ,则
,则![]() .即
.即![]() .解得
.解得![]() .
.
所以当![]() ,即
,即![]() 为
为![]() 中点时,
中点时,![]() 平面
平面![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
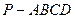 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD,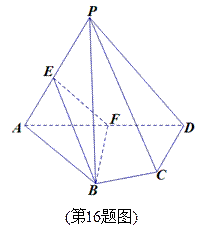
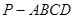 中,
中,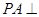 平面
平面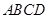 ,底面
,底面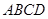 是菱形,
是菱形,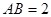 ,
,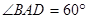 .
.
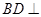
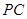 ;
;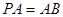 ,求二面角
,求二面角 的余弦值.
的余弦值. 中,
中, 平面
平面 ,底面
,底面 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.


 ,
, ………………2分
………………2分 ,得证。
,得证。 ,只要
,只要
 ,即
,即 ………6分
………6分
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以

 ………………3分
………………3分
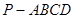 中,
中,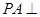 平面
平面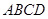 ,
,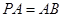
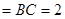 ,
,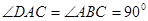 ,
,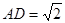 .
.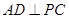 ;
;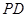 与平面
与平面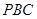 所成角的大小.
所成角的大小.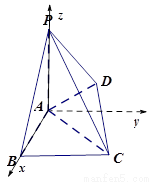
 中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点