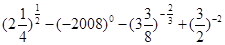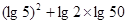题目内容
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量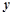 (件)与销售单价
(件)与销售单价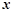 (元/件)可近似看作一次函数
(元/件)可近似看作一次函数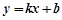 的关系(如图所示).
的关系(如图所示). 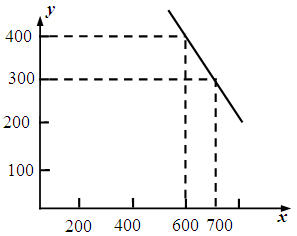
(1)根据图象,求一次函数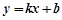 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价—成本总价)为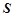 元. 试用销售单价
元. 试用销售单价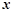 表示毛利润
表示毛利润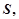 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
(1)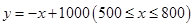 ;(2)当
;(2)当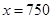 时,
时,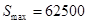 ,此时
,此时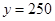 .
.
解析试题分析:(1)由于为一次函数所以只需从图中找两点坐标代入即可;(2)销售总价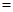 销售单价
销售单价 销售量,成本总价
销售量,成本总价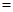 成本单价
成本单价 销售量,得毛利润
销售量,得毛利润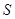 为关于
为关于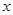 的一元二次函数注意
的一元二次函数注意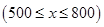 ,为二次函数给定区间求最值问题.
,为二次函数给定区间求最值问题.
试题解析:⑴由图象知,当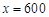 时,
时,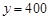 ;当
;当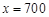 时,
时,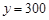 ,
,
分别代入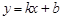 ,解得
,解得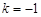 ,
, ,
,
所以 . 6分
. 6分
⑵销售总价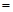 销售单价
销售单价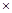 销售量
销售量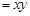 ,成本总价
,成本总价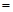 成本单价
成本单价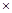 销售量
销售量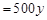 ,
,
代入求毛利润的公式,得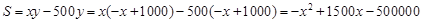 10分
10分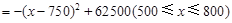 ,
,
当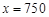 时,
时, ,此时
,此时 . 14分
. 14分
答:当销售单价为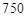 元/件时,可获得最大毛利润为
元/件时,可获得最大毛利润为 元,此时销售量为
元,此时销售量为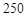 件. 16分
件. 16分
考点:1.函数的实际应用问题;2.二次函数求最值.

练习册系列答案
相关题目
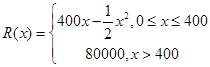 ,其中
,其中 是仪器的月产量.
是仪器的月产量.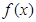 表示为月产量
表示为月产量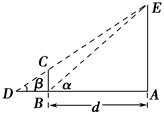
 ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).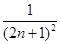 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|< .
.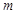 吨收取的污水处理费
吨收取的污水处理费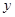 元,运行程序如下所示:请写出y与m的函数关系,并求排放污水150吨的污水处理费用.
元,运行程序如下所示:请写出y与m的函数关系,并求排放污水150吨的污水处理费用.
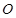 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为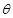 (弧度).
(弧度).
 ,求
,求