题目内容
设数列{an}的前n项积为Tn,且Tn=2-2an(n∈N*).
(1)求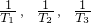 ,并证明
,并证明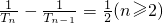 ;
;
(2)设bn=(1-an)(1-an+1),求数列{bn}的前n项和Sn.
解:(1)令n=1,可得T1=a1=2-2a1, ;
;
 ,
,
 ;
;
由题意可得: Tn•Tn-1=2Tn-1-2Tn(n≥2),
Tn•Tn-1=2Tn-1-2Tn(n≥2),
所以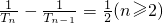 ;
;
(2)数列 为等差数列,
为等差数列, ,
,
当n≥2时, ,,当n=1时,
,,当n=1时,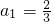 也符合,所以
也符合,所以 .
.
 =
= ,
,
∴ =
= =
= .
.
分析:(1)由Tn=a1•a2…an,Tn=2-2an可以求得a1,a2,a3,继而可求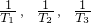 ,又
,又 ,结论易证;
,结论易证;
(2)由(1)知道, ,又bn=(1-an)(1-an+1),可以求得
,又bn=(1-an)(1-an+1),可以求得 ,从而可以求得sn.
,从而可以求得sn.
点评:本题重点考查数列的通项与数列求和,解题的关键是合理转化条件,转化为等差数列来解决,求和时的难点在于裂项法求和,出现正负项相消,从而问题解决.
 ;
; ,
,
 ;
;由题意可得:
 Tn•Tn-1=2Tn-1-2Tn(n≥2),
Tn•Tn-1=2Tn-1-2Tn(n≥2),所以
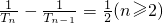 ;
;(2)数列
 为等差数列,
为等差数列, ,
,当n≥2时,
 ,,当n=1时,
,,当n=1时,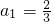 也符合,所以
也符合,所以 .
. =
= ,
,∴
 =
= =
= .
.分析:(1)由Tn=a1•a2…an,Tn=2-2an可以求得a1,a2,a3,继而可求
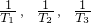 ,又
,又 ,结论易证;
,结论易证;(2)由(1)知道,
 ,又bn=(1-an)(1-an+1),可以求得
,又bn=(1-an)(1-an+1),可以求得 ,从而可以求得sn.
,从而可以求得sn.点评:本题重点考查数列的通项与数列求和,解题的关键是合理转化条件,转化为等差数列来解决,求和时的难点在于裂项法求和,出现正负项相消,从而问题解决.

练习册系列答案
相关题目