题目内容
已知a>0且a≠1,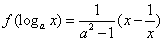 。
。
(1)求函数f(x)的解析式;
(2)试判定函数f(x)的奇偶性与单调性;
(3)若对于函数f(x),当x∈(-1,1)时,有f(1-m)+f(3m-2)<0恒成立,求实数m的取值范围.
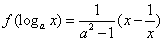 。
。(1)求函数f(x)的解析式;
(2)试判定函数f(x)的奇偶性与单调性;
(3)若对于函数f(x),当x∈(-1,1)时,有f(1-m)+f(3m-2)<0恒成立,求实数m的取值范围.
解:(1)令 ,则
,则 ,得
,得 ,
,
所以, 。
。
(2)因为 ,
,
所以函数f(x)为奇函数,
任取 ,则
,则 ,
,
因为当a>0且a≠1,恒有 ,所以f(x)为增函数。
,所以f(x)为增函数。
(3)因为f(x)为奇函数,所以由f(1-m)+f(3m-2)<0得,f(1-m)<-f(3m-2)=f(2-3m),
又f(x)为增函数,
所以,有 ,解得:
,解得: ,
,
所以,实数m的取值范围是( ,
, )。
)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目