题目内容
已知m，n是正数，证明：
≥m2+n2．
【答案】分析：不等式两边同乘mn，然后利用作差法进行化简，最后因式分解判定符号，即可证得结论．
解答：证明：两边同乘mn，得
m4+n4≥m3n+n3m，m，n＞0
作差得，m4+n4-m3n-n3m=m3（m-n）+n3（n-m）=（m3-n3）（m-n）=（m-n）2（m2+mn+n2）≥0，
∴
≥m2+n2．
点评：本题主要考查了不等式的证明，同时考查了因式分解，属于中档题．
解答：证明：两边同乘mn，得
m4+n4≥m3n+n3m，m，n＞0
作差得，m4+n4-m3n-n3m=m3（m-n）+n3（n-m）=（m3-n3）（m-n）=（m-n）2（m2+mn+n2）≥0，
∴
≥m2+n2．点评：本题主要考查了不等式的证明，同时考查了因式分解，属于中档题．
练习册系列答案
相关题目
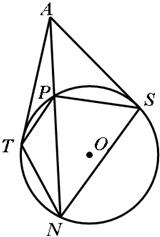选做题A．平面几何选讲
≥m2+n2．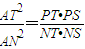
．
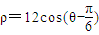上的动点，试求线段AB长的最大值．D．不等式选讲
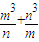≥m2+n2．