题目内容
关于x的不等式|ax+1|+a|x+1|≥3a.
(I)当a=1时,解上述不等式.
(II)当a<0时,若上述不等式恒成立,求实数a的取值范围.
解:(I)当a=1时,不等式|ax+1|+a|x+1|≥3a为2|x+1|≥3
∴x+1≥ 或x+1
或x+1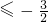
解得:{x|x≤- 或x≥
或x≥ }
}
(II)当a<0时,不等式|ax+1|+a|x+1|≥3a?-a|x+ |+a|x+1|≥3a?|x+1|-|x+
|+a|x+1|≥3a?|x+1|-|x+ |≤3恒成立根据绝对值的几何意义得|-1+
|≤3恒成立根据绝对值的几何意义得|-1+ |≤3?1-
|≤3?1- ≤3,解得a≤-
≤3,解得a≤- .
.
分析:(I)把a=1代入不等式|ax+1|+a|x+1|≥3a,根据绝对值不等式的解法解不等式;
(II)当a<0时,把不等式|ax+1|+a|x+1|≥3a等价变形为|x+1|-|x+ |≤3恒成立,根据绝对值不等式的几何意义求最值.
|≤3恒成立,根据绝对值不等式的几何意义求最值.
点评:考查应用绝对值的几何意义求最值,体现了转化的思想,而对于含有参数的问题,增加了试题的难度,属中等题.
∴x+1≥
 或x+1
或x+1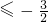
解得:{x|x≤-
 或x≥
或x≥ }
}(II)当a<0时,不等式|ax+1|+a|x+1|≥3a?-a|x+
 |+a|x+1|≥3a?|x+1|-|x+
|+a|x+1|≥3a?|x+1|-|x+ |≤3恒成立根据绝对值的几何意义得|-1+
|≤3恒成立根据绝对值的几何意义得|-1+ |≤3?1-
|≤3?1- ≤3,解得a≤-
≤3,解得a≤- .
.分析:(I)把a=1代入不等式|ax+1|+a|x+1|≥3a,根据绝对值不等式的解法解不等式;
(II)当a<0时,把不等式|ax+1|+a|x+1|≥3a等价变形为|x+1|-|x+
 |≤3恒成立,根据绝对值不等式的几何意义求最值.
|≤3恒成立,根据绝对值不等式的几何意义求最值.点评:考查应用绝对值的几何意义求最值,体现了转化的思想,而对于含有参数的问题,增加了试题的难度,属中等题.

练习册系列答案
相关题目