题目内容
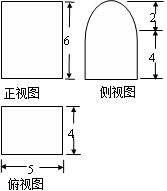
一个几何体的三视图如图所示（单位长度：
），俯视图中圆与四边形相切，且该几何体的体积为
，则该几何体的高
为( )
A． | B． |
C． | D． |
D
解析试题分析：由如图所示的几何体的三视图知：这个几何体是一个半径为
的球和一个直四棱柱的结合体，且这个直四棱柱的底面是对角线分别为
和
的棱形，这个直四棱柱的高为
，∴这个几何体的体积：V=
，
解得h=
.故选D.
考点：1.三视图；2.几何体的面积和体积
练习册系列答案
相关题目
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（ ）
A．外接球的半径为 | B．体积为 |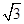
C．表面积为 | D．外接球的表面积为 |
如图是一几何体的三视图，则该几何体的表面积是( )
A． | B． | C． | D． |
已知某几何体的三视图如图所示，则该几何体的表面积等于（ ）
A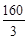． | B．160 | C． | D． |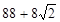
．正三棱锥的底边长和高都是2，则此正三棱锥的斜高长度为（ ）
A． | B． | C． | D． |
