题目内容
已知实数对(α,β),任取α,β∈{1,3,5},则使得sinα•cosβ<0的概率是( )
分析:当sinα>0 且cosβ<0 时,α=1,3,β=3,(α,β)共有2个;当sinα<0 且cosβ>0时,α=5,β=1,5,(α,β)共有2个.
解答:解:∵sinα•cosβ<0,∴sinα>0 且cosβ<0 ①,或sinα<0 且cosβ>0 ②.
若①成立,则 α=1,3,β=3,(α,β)共有2个.
若②成立,则 α=5,β=1,5,(α,β)共有2个,
综上,满足条件的(α,β)共4个,
而总数为9个,则使得sinα•cosβ<0的概率是
.
故选B.
若①成立,则 α=1,3,β=3,(α,β)共有2个.
若②成立,则 α=5,β=1,5,(α,β)共有2个,
综上,满足条件的(α,β)共4个,
而总数为9个,则使得sinα•cosβ<0的概率是
| 4 |
| 9 |
故选B.
点评:本题考查几何概型,考查正弦、余弦在各个象限内的符号,体现了分类讨论的数学思想.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
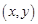 满足不等式组
满足不等式组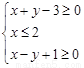 ,二元函数
,二元函数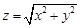 的最大值为( )
的最大值为( ) 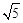 B.
B.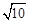 C.
C. D.
D.