Question

（2013•兰州一模）如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）若PA=AB，求棱锥C-PBD的高．

Answer 1

分析：（Ⅰ）利用线面垂直的判定定理证明BD⊥平面PAC；
（Ⅱ）利用等积法求棱锥C-PBD的高．

解答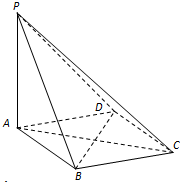：解：（Ⅰ）证明：因为四边形ABCD是菱形，所以AC⊥BD．
又因为PA⊥平面ABCD，所以PA⊥BD．
又PA∩AC=A，所以BD⊥平面PAC．…（6分）
（Ⅱ）解：∵V_C-PBD=V_P-CBD，设棱锥C-PBD的高为h，
∴

1

3

h?S△PBD=

1

3

PA?S△CBD   …（8分）
∵PA=AB，AB=2，∠BAD=60°，
∴PB=PD=2

2

，BD=2
∴S△PBD=

1

2

BD?

PB2-( 1 2 BD)2

=

7

，S△CBD=

1

2

BD?

1

2

AC=

3

，…（10分）
∴h=

PA?S△CBD

S△PBD

=

2 21

7

．
即棱锥C-PBD的高为

2 21

7

．…（12分）

点评：本题主要考查空间线面垂直的判定以及空间距离的求法，利用相应的判定定理是解决本题的关键．