题目内容
已知函数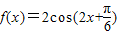 ,下面四个结论中正确的是( )
,下面四个结论中正确的是( )A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于直线
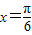 对称
对称C.函数f(x)的图象是由y=2cos2x的图象向左平移
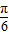 个单位得到
个单位得到D.函数
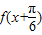 是奇函数
是奇函数
【答案】分析:由f(x)=2cos(2x+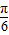 )可求得周期T=π,从而可判断A的正误;
)可求得周期T=π,从而可判断A的正误;
将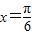 代入f(x)=2cos(2x+
代入f(x)=2cos(2x+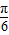 )可得f(
)可得f(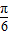 )的值,看是否为最大值或最小值,即可判断B的正误;
)的值,看是否为最大值或最小值,即可判断B的正误;
y=2cos2x的图象向左平移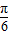 个单位得到y=2cos2(x+
个单位得到y=2cos2(x+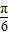 )=2cos(2x+
)=2cos(2x+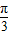 ),显然C不对;
),显然C不对;
f(x+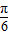 )=2cos(2x+
)=2cos(2x+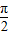 )=-2sinx,可判断D的正误.
)=-2sinx,可判断D的正误.
解答:解:∵f(x)=2cos(2x+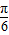 ),故周期T=π,可排除A;
),故周期T=π,可排除A;
将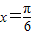 代入f(x)=2cos(2x+
代入f(x)=2cos(2x+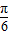 )可得:f(
)可得:f(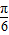 )=2cos
)=2cos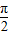 =0≠±2,故可排除B;
=0≠±2,故可排除B;
y=2cos2x的图象向左平移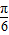 个单位得到y=2cos2(x+
个单位得到y=2cos2(x+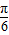 )=2cos(2x+
)=2cos(2x+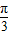 ),故可排除C;
),故可排除C;
f(x+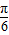 )=2cos(2x+
)=2cos(2x+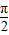 )=-2sinx,显然为奇函数,故D正确.
)=-2sinx,显然为奇函数,故D正确.
故选D.
点评:本题考查余弦函数的奇偶性与对称性及其周期的求法,关键是熟练掌握三角函数的性质,易错点在于函数图象的平移变换的判断,属于中档题.
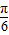 )可求得周期T=π,从而可判断A的正误;
)可求得周期T=π,从而可判断A的正误;将
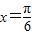 代入f(x)=2cos(2x+
代入f(x)=2cos(2x+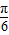 )可得f(
)可得f(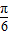 )的值,看是否为最大值或最小值,即可判断B的正误;
)的值,看是否为最大值或最小值,即可判断B的正误;y=2cos2x的图象向左平移
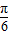 个单位得到y=2cos2(x+
个单位得到y=2cos2(x+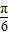 )=2cos(2x+
)=2cos(2x+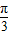 ),显然C不对;
),显然C不对;f(x+
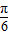 )=2cos(2x+
)=2cos(2x+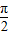 )=-2sinx,可判断D的正误.
)=-2sinx,可判断D的正误.解答:解:∵f(x)=2cos(2x+
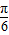 ),故周期T=π,可排除A;
),故周期T=π,可排除A;将
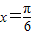 代入f(x)=2cos(2x+
代入f(x)=2cos(2x+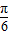 )可得:f(
)可得:f(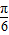 )=2cos
)=2cos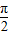 =0≠±2,故可排除B;
=0≠±2,故可排除B;y=2cos2x的图象向左平移
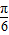 个单位得到y=2cos2(x+
个单位得到y=2cos2(x+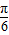 )=2cos(2x+
)=2cos(2x+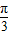 ),故可排除C;
),故可排除C;f(x+
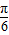 )=2cos(2x+
)=2cos(2x+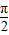 )=-2sinx,显然为奇函数,故D正确.
)=-2sinx,显然为奇函数,故D正确.故选D.
点评:本题考查余弦函数的奇偶性与对称性及其周期的求法,关键是熟练掌握三角函数的性质,易错点在于函数图象的平移变换的判断,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
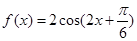 ,下面四个结论中正确的是 ( )
,下面四个结论中正确的是 ( )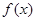 的最小正周期为
的最小正周期为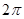
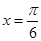 对称
对称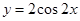 的图象向左平移
的图象向左平移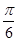 个单位得到
个单位得到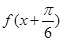 是奇函数
是奇函数 ,下面四个结论中正确的是( )
,下面四个结论中正确的是( ) 对称
对称 个单位得到
个单位得到 是奇函数
是奇函数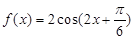 ,下面四个结论中正确的是( )
,下面四个结论中正确的是( )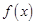 的最小正周期为
的最小正周期为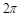
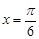 对称
对称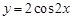 的图象向左平移
的图象向左平移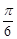 个单位得到
个单位得到 是奇函数
是奇函数 ,下面四个结论中正确的是
( )
,下面四个结论中正确的是
( )  的最小正周期为
的最小正周期为
 对称
对称 的图象向左平移
的图象向左平移 个单位得到
个单位得到
 是奇函数
是奇函数 ,下面四个结论中正确的是(
)
,下面四个结论中正确的是(
) 的最小正周期为
的最小正周期为
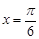 对称
对称 的图象向左平移
的图象向左平移 个单位得到
个单位得到 是奇函数
是奇函数