题目内容
已知函数f(x)=ax+ +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)试用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+ +
+ +L+
+L+ >ln(n+1)+
>ln(n+1)+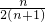 (n≥1).
(n≥1).
解:(1)∵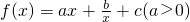 ,
,
∴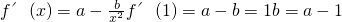
∴f(1)=a+a-1+c=2a-1+c.
又∵点(1,f(1))在切线y=x-1上,
∴2a-1+c=0?c=1-2a,
∴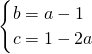 .
.
(2)∵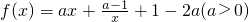 ,
,
f(x)≥lnx在[1,+∞]上恒成立,
设g(x)=f(x)-lnx,则g(x)=f(x)-lnx≥0在[1,+∞]上恒成立,
∴g(x)min≥0,
又∵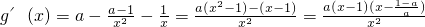 ,
,
而当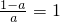 时,
时, .
.
1°当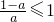 即
即 时,
时,
g'(x)≥0在[1,+∞]上恒成立,
∴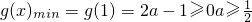 ;
;
2°当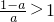 即
即 时,
时,
g'(x)=0时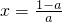 ;
;
且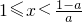 时,g'(x)<0,
时,g'(x)<0,
当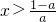 时,g'(x)>0;
时,g'(x)>0;
则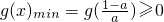 ①,
①,
又∵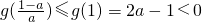 与①矛盾,不符题意,故舍.
与①矛盾,不符题意,故舍.
∴综上所述,a的取值范围为:[ ,+∞).
,+∞).
(3)证明:由(1)可知 时,f(x)≥lnx在[1,+∞]上恒成立,
时,f(x)≥lnx在[1,+∞]上恒成立,
则当 时,
时,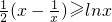 在[1,+∞]上恒成立,
在[1,+∞]上恒成立,
令x依次取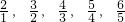 …
… 时,
时,
则有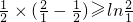 ,
,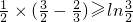 ,
,
…
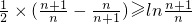 ,
,
由同向不等式可加性可得
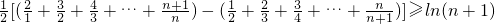 ,
,
即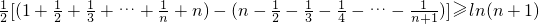 ,
,
也即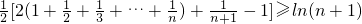 ,
,
也即1+ +
+ +…+
+…+ >ln(n+1)+
>ln(n+1)+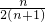 (n≥1).
(n≥1).
解法二:①当n=1时左边=1,右边=ln2+ <1,不等式成立;
<1,不等式成立;
②假设n=k时,不等式成立,就是1+ +
+ +…+
+…+ >ln(k+1)+
>ln(k+1)+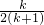 (k≥1).
(k≥1).
那么1+ +
+ +…+
+…+ +
+ >ln(k+1)+
>ln(k+1)+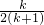 +
+
=ln(k+1)+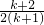 .
.
由(2)知:当 时,有f(x)≥lnx (x≥1)
时,有f(x)≥lnx (x≥1)
令 有f(x)=
有f(x)=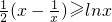 (x≥1)
(x≥1)
令x=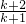 得
得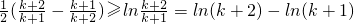
∴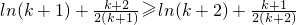
∴1+ +
+ +…+
+…+ +
+ >
>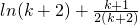
这就是说,当n=k+1时,不等式也成立.
根据(1)和(2),可知不等式对任何n∈N*都成立.
分析:(1)通过函数的导数,利用导数值就是切线的斜率,切点在切线上,求出b,c即可.
(2)利用f(x)≥lnx,构造g(x)=f(x)-lnx,问题转化为g(x)=f(x)-lnx≥0在[1,+∞]上恒成立,
利用导数求出函数在[1,+∞)上的最小值大于0,求a的取值范围;
(3)由(1)可知 时,f(x)≥lnx在[1,+∞]上恒成立,则当
时,f(x)≥lnx在[1,+∞]上恒成立,则当 时,
时,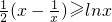 在[1,+∞]上恒成立,
在[1,+∞]上恒成立,
对不等式的左侧每一项裂项,然后求和,即可推出要证结论.
解法二:利用数学归纳法的证明步骤,证明不等式成立即可.
点评:本题是难题,考查函数与导数的关系,曲线切线的斜率,恒成立问题的应用,累加法与裂项法的应用,数学归纳法的应用等知识,知识综合能力强,方法多,思维量与运算良以及难度大,需要仔细审题解答,还考查分类讨论思想.
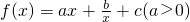 ,
,∴
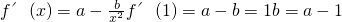
∴f(1)=a+a-1+c=2a-1+c.
又∵点(1,f(1))在切线y=x-1上,
∴2a-1+c=0?c=1-2a,
∴
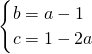 .
.(2)∵
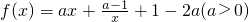 ,
,f(x)≥lnx在[1,+∞]上恒成立,
设g(x)=f(x)-lnx,则g(x)=f(x)-lnx≥0在[1,+∞]上恒成立,
∴g(x)min≥0,
又∵
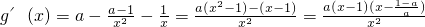 ,
,而当
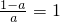 时,
时, .
.1°当
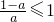 即
即 时,
时,g'(x)≥0在[1,+∞]上恒成立,
∴
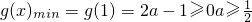 ;
;2°当
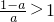 即
即 时,
时,g'(x)=0时
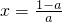 ;
;且
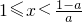 时,g'(x)<0,
时,g'(x)<0,当
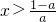 时,g'(x)>0;
时,g'(x)>0;则
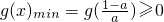 ①,
①,又∵
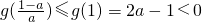 与①矛盾,不符题意,故舍.
与①矛盾,不符题意,故舍.∴综上所述,a的取值范围为:[
 ,+∞).
,+∞).(3)证明:由(1)可知
 时,f(x)≥lnx在[1,+∞]上恒成立,
时,f(x)≥lnx在[1,+∞]上恒成立,则当
 时,
时,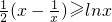 在[1,+∞]上恒成立,
在[1,+∞]上恒成立,令x依次取
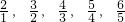 …
… 时,
时,则有
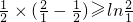 ,
,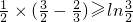 ,
,…
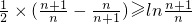 ,
,由同向不等式可加性可得
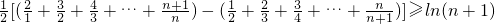 ,
,即
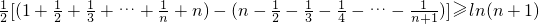 ,
,也即
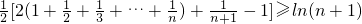 ,
,也即1+
 +
+ +…+
+…+ >ln(n+1)+
>ln(n+1)+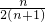 (n≥1).
(n≥1).解法二:①当n=1时左边=1,右边=ln2+
 <1,不等式成立;
<1,不等式成立;②假设n=k时,不等式成立,就是1+
 +
+ +…+
+…+ >ln(k+1)+
>ln(k+1)+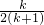 (k≥1).
(k≥1).那么1+
 +
+ +…+
+…+ +
+ >ln(k+1)+
>ln(k+1)+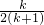 +
+
=ln(k+1)+
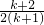 .
.由(2)知:当
 时,有f(x)≥lnx (x≥1)
时,有f(x)≥lnx (x≥1)令
 有f(x)=
有f(x)=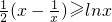 (x≥1)
(x≥1)令x=
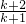 得
得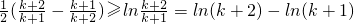
∴
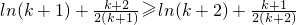
∴1+
 +
+ +…+
+…+ +
+ >
>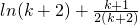
这就是说,当n=k+1时,不等式也成立.
根据(1)和(2),可知不等式对任何n∈N*都成立.
分析:(1)通过函数的导数,利用导数值就是切线的斜率,切点在切线上,求出b,c即可.
(2)利用f(x)≥lnx,构造g(x)=f(x)-lnx,问题转化为g(x)=f(x)-lnx≥0在[1,+∞]上恒成立,
利用导数求出函数在[1,+∞)上的最小值大于0,求a的取值范围;
(3)由(1)可知
 时,f(x)≥lnx在[1,+∞]上恒成立,则当
时,f(x)≥lnx在[1,+∞]上恒成立,则当 时,
时,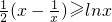 在[1,+∞]上恒成立,
在[1,+∞]上恒成立,对不等式的左侧每一项裂项,然后求和,即可推出要证结论.
解法二:利用数学归纳法的证明步骤,证明不等式成立即可.
点评:本题是难题,考查函数与导数的关系,曲线切线的斜率,恒成立问题的应用,累加法与裂项法的应用,数学归纳法的应用等知识,知识综合能力强,方法多,思维量与运算良以及难度大,需要仔细审题解答,还考查分类讨论思想.

练习册系列答案
相关题目