题目内容
如图,已知正四棱柱ABCD-A1B1C1D1的底面边长为4,A1A=6,Q为B1B的中点,P∈DD1,M∈A1B1,N∈C1D1,A1M=1,D1N=3.
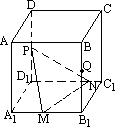
①当P为DD1中点时,求二面角M-PN-D1的大小;
②DD1上是否存在点P,使QD1⊥面PMN?若存在,求出P点的位置,若不存在,说明理由.
③若P为DD1中点,求三棱锥Q-PMN体积.
答案:
解析:
解析:
|
①过M做MO⊥D1C1,过O作OH⊥PN,边MH,则∠MHO为二面角M-PN-D1的平面角,易求∠MHO=arccos ②不存在,因为假设存在点P使QP1⊥平面PMN,则QD1⊥MN,QD1在底面上的射影为B1D1,则B1D1⊥MN,而实际B1D1不垂直MN. ③易知VQ-PMN=2VB |

练习册系列答案
相关题目

 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a. 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.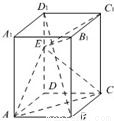 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.