题目内容
已知 ,当
,当 时,均有
时,均有 ,则实数a的取值范围为 .
,则实数a的取值范围为 .
【答案】分析:先通过移项分离成两个函数,然后问题就转化为一个函数的最大值小于另一个函数的最小值的问题,然后分底数大于0小于1和大于1两种情况进行求解,综合两种情况就可得出a的范围.
解答:解:由题意即:x ,
, 恒成立
恒成立
? ,
, ①恒成立
①恒成立
令h(x)= ,g(x)=ax
,g(x)=ax
问题转化为h(x)的最大值小于g(x)的最小值
∵h(x)= 在
在 上单调递减,∴当x=
上单调递减,∴当x= 时,
时,
当0<a<1时,g(x)在 上单调递减,∴
上单调递减,∴ ,∵
,∵ ,此时不等式①不能恒成立
,此时不等式①不能恒成立
当a>1时,g(x)在 上单调递增,∴
上单调递增,∴ ,要使①恒成立,则
,要使①恒成立,则  ,∴
,∴
综上所述,
故答案为:
点评:本题主要考查了函数恒成立问题,一般方法是分离常数之后构造函数,转化为函数求最值问题,但本题无法分离常数,所以分离为两个常见函数,转化为两个函数的最值关系问题.
解答:解:由题意即:x
 ,
, 恒成立
恒成立?
 ,
, ①恒成立
①恒成立令h(x)=
 ,g(x)=ax
,g(x)=ax问题转化为h(x)的最大值小于g(x)的最小值
∵h(x)=
 在
在 上单调递减,∴当x=
上单调递减,∴当x= 时,
时,
当0<a<1时,g(x)在
 上单调递减,∴
上单调递减,∴ ,∵
,∵ ,此时不等式①不能恒成立
,此时不等式①不能恒成立当a>1时,g(x)在
 上单调递增,∴
上单调递增,∴ ,要使①恒成立,则
,要使①恒成立,则  ,∴
,∴
综上所述,

故答案为:

点评:本题主要考查了函数恒成立问题,一般方法是分离常数之后构造函数,转化为函数求最值问题,但本题无法分离常数,所以分离为两个常见函数,转化为两个函数的最值关系问题.

练习册系列答案
相关题目
 且
且 ,函数
,函数 ,当
,当 时,均有
时,均有 ,则实数
,则实数 的取值范围是
的取值范围是  B.
B.

 D.
D.

 且
且 ,函数
,函数 ,当
,当 时,均有
时,均有 ,则实数
,则实数 的取值范围是
的取值范围是  B.
B.

 D.
D.

 ,当
,当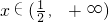 时,均有
时,均有 ,则实数a的取值范围为________.
,则实数a的取值范围为________.