Question

【题目】已知函数的图象在处的切线方程为，其中是自然对数的底数.

（1）若对任意的，都有成立，求实数的取值范围；

（2）若函数的两个零点为，试判断的正负，并说明理由.

Answer 1

【答案】（1）.（2）见解析

【解析】试题分析：（1）由解得.由题可得在恒成立，分别求得两边函数的值域，运用恒成立思想，即可得到k的范围

（2）由题意知，函数， 是函数的两个零点，易得函数在区间在区间上单调递减.只需证明即可.

试题解析： （1）由题得， ，

∵函数在处的切线方程为，

∴，∴.

依题意， 对任意的都成立，

∴，即对任意的都成立，从而.

又不等式整理可得， .

令，

∴ .

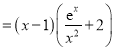令，得，

当时， ， 单调递减；

当时， ， 单调递增.

∴.

综上所述，实数的取值范围为.

（2）结论是.

理由如下：由题意知，函数，

∴，

易得函数在区间上单调递增，在区间上单调递减.

∴只需证明即可.

∵是函数的两个零点，

∴相减，得.

不妨令，

则，∴，

∴， ，

即证，

即证.

∵ ，

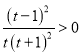∴在区间上单调递增.

∴.

综上所述，函数总满足.