题目内容
对任意实数x、y,定义运算x*y=ax+by+cxy,其中a、b、c为常实数,等号右边的运算是通常意义的加、乘运算.现已知2*1=3,2*3=4,且有一个非零实数m,使得对任意实数x,都有x*m=2x,则m=
3
3
.分析:由题意构造方程组,不难得到参数a,b,c之间的关系.再由x*m=2x,可以得到一个关于m的方程,解方程即可求出满足条件的m的值.
解答:解:∵x*y=ax+by+cxy,
由1*2=3,2*3=4,得
解得b=2+2c,a=-1-6c.
又由x*m=ax+bm+cmx=2x对于任意实数x恒成立,
∴
,
∵m为非零实数,∴b=0=2+2c,∴c=-1.
∴(-1-6c)+cm=2,∴-1+6-m=2.
解得m=3.
故答案为:3
由1*2=3,2*3=4,得
|
解得b=2+2c,a=-1-6c.
又由x*m=ax+bm+cmx=2x对于任意实数x恒成立,
∴
|
∵m为非零实数,∴b=0=2+2c,∴c=-1.
∴(-1-6c)+cm=2,∴-1+6-m=2.
解得m=3.
故答案为:3
点评:本题考查新定义,根据新运算的定义,将已知中的数据代入进行运算即可得最终结果,属基础题.

练习册系列答案
相关题目

 +2at)x+3at+b=0,直线l的
+2at)x+3at+b=0,直线l的 ,则当t为何值时,f(t)有最大值,最大值是多少?
,则当t为何值时,f(t)有最大值,最大值是多少? )在曲线C上,又在直线l上,求
)在曲线C上,又在直线l上,求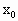 的取值范围.
的取值范围. .
.