题目内容
(本小题满分13分)
动圆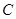 与定圆
与定圆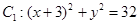 内切,与定圆
内切,与定圆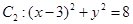 外切,A点坐标为
外切,A点坐标为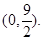
(1)求动圆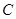 的圆心
的圆心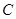 的轨迹方程和离心率;
的轨迹方程和离心率;
(2)若轨迹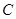 上的两点
上的两点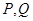 满足
满足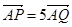 ,求
,求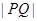 的值.
的值.
【答案】
(1)由椭圆的定义知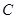 点的轨迹是以
点的轨迹是以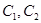 为焦点,长轴长为
为焦点,长轴长为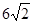 的椭圆,其轨迹方程为
的椭圆,其轨迹方程为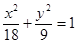 ,离心率为
,离心率为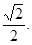 ;(2)
;(2)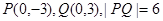 .
.
【解析】本试题主要是考查了运用定义法求解轨迹方程以及直线与圆锥曲线的位置关系的综合运用。
(1)利用圆与圆的位置关系,结合圆心距和半径的关系,得到动点的轨迹满足椭圆的定义,然后结合定义得到轨迹方程。
(2)设出直线方程与椭圆方程联立方程组,然后结合韦达定理和向量的关系式的,到坐标关系,进而化简得到点的坐标。
(1)如图,设动圆C的半径为R,
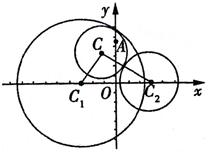
则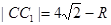 ,①
,①
 ,②
,②
①+②得,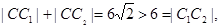
由椭圆的定义知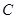 点的轨迹是以
点的轨迹是以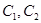 为焦点,长轴长为
为焦点,长轴长为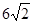 的椭圆,其轨迹方程为
的椭圆,其轨迹方程为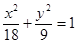 ,离心率为
,离心率为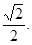 ……………………………………………………………………6分
……………………………………………………………………6分
(2)设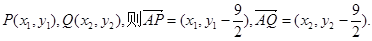
由 可得
可得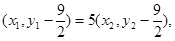
所以 ③…………………………………9分
③…………………………………9分
由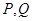 是椭圆
是椭圆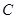 上的两点,得
上的两点,得
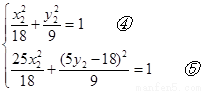 ,由④、⑤得
,由④、⑤得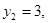
将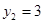 代入③,得
代入③,得 ,将
,将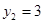 代入④,得
代入④,得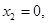 所以
所以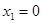 ,
,
所以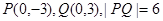 .……………………………………………………13分
.……………………………………………………13分

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和