题目内容
用数学归纳法证明: (n≥2,n∈N*)的过程中,从“k到k+1”左端需增加的代数式为
(n≥2,n∈N*)的过程中,从“k到k+1”左端需增加的代数式为
- A.
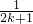
- B.
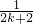
- C.

- D.

D
分析:先看出所给的不等式的左边的结构式,看出左边的分母是从n+1变化到n+n,写出当n=k时和n=k+1时的不等式,把写出的不等式相减,得到结论.
解答:∵用数学归纳法证明: ,
,
当n=k(k≥2)时,有
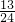
那么当n=k+1时,左边=
=
∴从“k到k+1”左端需增加的代数式为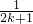 +
+ =
= ,
,
故选D
点评:本题考查用数学归纳法来证明不等式,本题解题的关键是看出不等式的结构形式,写出不等式的结构以后才能看出两边的差距,本题是一个中档题目.
分析:先看出所给的不等式的左边的结构式,看出左边的分母是从n+1变化到n+n,写出当n=k时和n=k+1时的不等式,把写出的不等式相减,得到结论.
解答:∵用数学归纳法证明:
 ,
,当n=k(k≥2)时,有

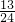
那么当n=k+1时,左边=

=

∴从“k到k+1”左端需增加的代数式为
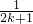 +
+ =
= ,
,故选D
点评:本题考查用数学归纳法来证明不等式,本题解题的关键是看出不等式的结构形式,写出不等式的结构以后才能看出两边的差距,本题是一个中档题目.

练习册系列答案
相关题目